题目内容
已知:以点C (t,  )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(Ⅰ)求证:△OAB的面积为定值;
(Ⅱ)设直线y = –2x+4与圆C交于点M, N,若|OM| = |ON|,求圆C的方程.
(1)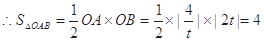 (2)
(2)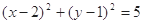
解析试题分析:解 (1)
 ,
,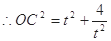 .
.
设圆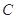 的方程是
的方程是 
令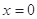 ,得
,得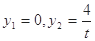 ;令
;令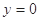 ,得
,得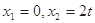
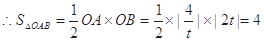 ,即:
,即: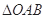 的面积为定值.……5分
的面积为定值.……5分
(2)
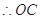 垂直平分线段
垂直平分线段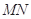 .
.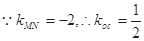 ,
,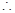 直线
直线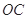 的方程是
的方程是 .
. ,解得:
,解得: ……7分
……7分
当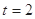 时,圆心
时,圆心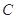 的坐标为
的坐标为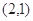 ,
,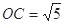 ,
,
此时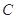 到直线
到直线
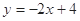 的距离
的距离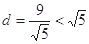 ,
,
圆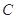 与直线
与直线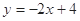 相交于两点. ……10分
相交于两点. ……10分
当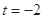 时,圆心
时,圆心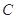 的坐标为
的坐标为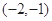 ,
,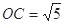 ,
,
此时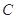 到直线
到直线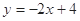 的距离
的距离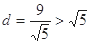 圆
圆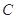 与直线
与直线
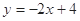 不相交,
不相交,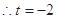 不符合题意舍去.
不符合题意舍去.
圆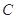 的方程为
的方程为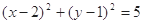 ……10分
……10分
考点:三角形的面积,圆的方程
点评:解决的关键是根据截距来得到面积的表示,以及借助于圆心和半径求解圆的方程,属于基础题。

练习册系列答案
相关题目
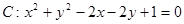 ,直线
,直线  ,
, 与圆
与圆 交与
交与 两点,点
两点,点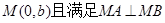 .
. 时,求
时,求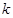 的值;
的值;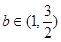 时,求
时,求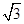 ,半径小于5.
,半径小于5. 和圆
和圆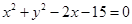 相交于点
相交于点 。
。 的垂直平分线方程;(2)求弦
的垂直平分线方程;(2)求弦 经过点
经过点 ,且和圆
,且和圆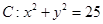 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-
 的取值范围.
的取值范围. ,圆
,圆 .
.
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 同时平分圆
同时平分圆 中,直线
中,直线 截以原点
截以原点 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为
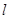 与圆
与圆 ,当
,当 长最小时,求直线
长最小时,求直线 的直线
的直线 ,使
,使 ,以
,以 和直线
和直线
 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;