题目内容
如图，已知圆
，圆
．
（1）若过点
的直线
被圆
截得的弦长为
，求直线的方程；
（2）设动圆
同时平分圆、圆的周长．
①求证：动圆圆心在一条定直线上运动；
②动圆是否过定点？若过，求出定点的坐标；若不过，请说明理由．
（1）
或
（2）①求出圆心的轨迹方程为直线
即可；
②动圆过定点
和
解析试题分析：（1）由题意可知
，
，
，
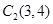由图知直线的斜率一定存在，设直线的方程为
，即
因为直线被圆截得的弦长为，所以圆心到直线的距离为
……3分
解得
或
，所以直线的方程为或． ……6分
（2）①证明：设动圆圆心
，由题可知
则
化简得，所以动圆圆心在定直线上运动． ……10分
②动圆过定点
设
，则动圆的半径为
动圆的方程为
整理得
……14分
，解得
或
所以动圆过定点和． ……16分
考点：本小题主要考查直线与圆的位置关系.
点评：求解直线与圆的位置关系，主要看圆心到直线的距离与半径的关系，设直线方程时要注意直线的适用条件.
练习册系列答案
科学实验活动册系列答案
相关题目
是抛物线
上的点，
是
的焦点， 以
为直径的圆
与
轴的另一个交点为
.
且斜率大于零的直线
与抛物线
两点，
为坐标原点，
的面积为
，证明：直线
，
交于A、B两点；
上的圆的方程.
)(t∈R , t ≠ 0)为圆心的圆与
轴交于点O, A，与y轴交于点O, B，其中O为原点．
，直线
：
.
时，求直线
经过点
，且和圆
相交，截得的弦长为4
，求直线
直线
.
相切, 且与直线
平行的直线
的方程;
与圆
轴上的截距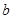
的取值范围.
和定点
，由圆
外一点
向圆
，切点为
，且满足
，
间满足的等量关系；
.
相交于M、N两点，且OM⊥ON（O为坐标原点），求m；