题目内容
已知实数x、y、z满足3x=4y=6z>1.
(1)求证: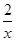 +
+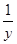 =
=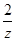 ;
;
(2)试比较3x、4y、6z的大小.
(1)求证:
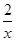 +
+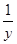 =
=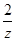 ;
;(2)试比较3x、4y、6z的大小.
(1)见解析(2)3x<4y<6z
(1)证明:令k=3x=4y=6z>1,则x=log3k,y=log4k,z=log6k,
于是 =logk3,
=logk3,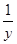 =logk4,
=logk4, =logk6,从而
=logk6,从而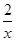 +
+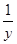 =2logk3+logk4=logk32+logk4=logk36=2logk6,等式成立.
=2logk3+logk4=logk32+logk4=logk36=2logk6,等式成立.
(2)解:由于k>1,故x、y、z>0.


故3x<4y<6z.
于是
 =logk3,
=logk3,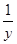 =logk4,
=logk4, =logk6,从而
=logk6,从而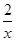 +
+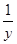 =2logk3+logk4=logk32+logk4=logk36=2logk6,等式成立.
=2logk3+logk4=logk32+logk4=logk36=2logk6,等式成立.(2)解:由于k>1,故x、y、z>0.


故3x<4y<6z.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
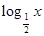 ,h(x)=log2x-
,h(x)=log2x-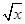 的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是______________.
的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是______________. 的图像与
的图像与 轴有公共点,则
轴有公共点,则 的取值范围是( )
的取值范围是( )



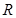 上的奇函数
上的奇函数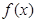 满足:当
满足:当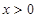 时,
时,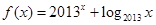 ,则方程
,则方程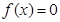 的实数根的个数是( )
的实数根的个数是( ) ,P4(2,2)中,“好点”的个数为( )
,P4(2,2)中,“好点”的个数为( ) 在
在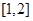 上的最大值比最小值大
上的最大值比最小值大 ,则
,则 .
. ,则( )
,则( )


