题目内容
设函数f(x)＝ex＋x－2，g(x)＝lnx＋x2－3.若实数a、b满足f(a)＝0，g(b)＝0，则g(a)、f(b)、0三个数的大小关系为________．
g(a)<0<f(b)
易知f(x)是增函数，g(x)在(0，＋∞)上也是增函数，由于f(a)＝0，而f(0)＝－1<0，f(1)＝e－1>0，所以0<a<1；又g(1)＝－2<0，g(2)＝ln2＋1>0，所以1<b<2，所以f(b)>0，g(a)<0，故g(a)<0<f(b)．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
＋
＝
；
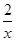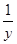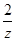，则
= .
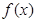在D内是单调函数；②存在[a，b]上的值域为
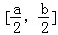，那么就称函数
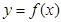为“成功函数”，若函数
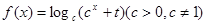是“成功函数”，则t的取值范围为（ ）
)|1-x|+m的图象与x轴有公共点,则m的取值范围是( )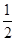
时，4x<logax，则实数a的取值范围是________．
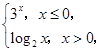则f(f(0))＝________．