题目内容
已知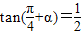 ,求值:
,求值:(1)tanα;
(2)
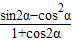 .
.
【答案】分析:(1)由题意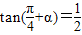 ,可由正切的和角公式展开得
,可由正切的和角公式展开得 ,由此方程解出tanα;
,由此方程解出tanα;
(2)由正弦与余弦的二倍角公式将 这形为
这形为 ,再由同角三角关系,将其变为
,再由同角三角关系,将其变为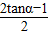 将正切值代入即可求出代数式的值.
将正切值代入即可求出代数式的值.
解答:解:(1)由题意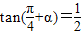 ,可得
,可得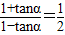 ,解得tanα=-
,解得tanα=-
(2)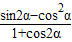 =
=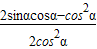 =
=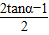
由(1)tanα=- ,
,
∴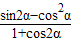 =
=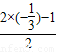 =-
=-
点评:本题考查了两角的和的正切公式,正弦、余弦的二倍角公式,同角三角函数的基本关系,解题的关键是牢固记忆公式,能根据这些公式灵活变形,求出代数式的值,三角函数由于公式多,可选择的方法多,故解题时要注意选取最合适的方法解题
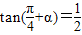 ,可由正切的和角公式展开得
,可由正切的和角公式展开得 ,由此方程解出tanα;
,由此方程解出tanα;(2)由正弦与余弦的二倍角公式将
 这形为
这形为 ,再由同角三角关系,将其变为
,再由同角三角关系,将其变为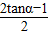 将正切值代入即可求出代数式的值.
将正切值代入即可求出代数式的值.解答:解:(1)由题意
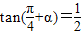 ,可得
,可得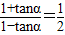 ,解得tanα=-
,解得tanα=-
(2)
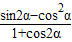 =
=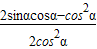 =
=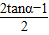
由(1)tanα=-
 ,
,∴
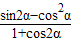 =
=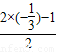 =-
=-
点评:本题考查了两角的和的正切公式,正弦、余弦的二倍角公式,同角三角函数的基本关系,解题的关键是牢固记忆公式,能根据这些公式灵活变形,求出代数式的值,三角函数由于公式多,可选择的方法多,故解题时要注意选取最合适的方法解题

练习册系列答案
相关题目
 如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)