题目内容
 (2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=
(2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=| 2 |
(1)求证:AG⊥平面BCEF
(2)求DG的长度.
分析:(1)根据翻折后EF⊥AF,EF⊥BF,可得EF⊥平面ABF,所以EF⊥AG,结合等边△ABF中AG⊥BF,利用线面垂直的判定定理,即可证出AG⊥平面BCEF;
(2)取EC中点M,连接MC、MD、MG,可证出平面DCE∥平面ABF,从而AG∥DM,得到DM⊥平面BCEF.再在梯形BFEC中证出四边形EFGC是平行四边形,从而EF∥CG.然后在Rt△BCG中,算出CG=1,在Rt△GCM中,算出GM=
,最后在Rt△GDM中,得到DG=
.
(2)取EC中点M,连接MC、MD、MG,可证出平面DCE∥平面ABF,从而AG∥DM,得到DM⊥平面BCEF.再在梯形BFEC中证出四边形EFGC是平行四边形,从而EF∥CG.然后在Rt△BCG中,算出CG=1,在Rt△GCM中,算出GM=
| ||
| 2 |
| 2 |
解答:解:(1)∵AF=BF且∠AFB=60°,
∴△ABF是等边三角形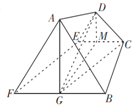
又∵G是FB的中点,∴AG⊥BF
∵翻折前的等腰梯形ABCD中,E、F分别是CD、AB的中点,
∴EF⊥AB,可得翻折后EF⊥AF,EF⊥BF
∵AF、BF是平面ABF内的相交直线,∴EF⊥平面ABF
∵AG?平面ABF,∴AG⊥EF,
∵BF、EF是平面BCEF内的相交直线,
∴AG⊥平面BCEF
(2)取EC中点M,连接MC、MD、MG
∵AF∥DE,AF?平面ABF,DE?平面ABF,∴DE∥平面ABF,同理可得:CE∥平面ABF,
∵DE、CE是平面DCE内的相交直线,∴平面DCE∥平面ABF,可得AG∥DM
∵AG⊥平面BCEF,∴DM⊥平面BCEF,
∵MG?平面BCEF,∴DM⊥MG,
∵梯形BFEC中,EC=FG=BG=1,BF∥EC,∴四边形EFGC是平行四边形,可得EF∥CG
∵EF⊥平面ABF,∴CG⊥平面ABF,可得CG⊥BG
Rt△BCG中,BG=1,BC=
,可得CG=
=1
∴Rt△GCM中,GM=
=
又∵DM=
CE=
,
∴Rt△GDM中,DG=
=
∴△ABF是等边三角形

又∵G是FB的中点,∴AG⊥BF
∵翻折前的等腰梯形ABCD中,E、F分别是CD、AB的中点,
∴EF⊥AB,可得翻折后EF⊥AF,EF⊥BF
∵AF、BF是平面ABF内的相交直线,∴EF⊥平面ABF
∵AG?平面ABF,∴AG⊥EF,
∵BF、EF是平面BCEF内的相交直线,
∴AG⊥平面BCEF
(2)取EC中点M,连接MC、MD、MG
∵AF∥DE,AF?平面ABF,DE?平面ABF,∴DE∥平面ABF,同理可得:CE∥平面ABF,
∵DE、CE是平面DCE内的相交直线,∴平面DCE∥平面ABF,可得AG∥DM
∵AG⊥平面BCEF,∴DM⊥平面BCEF,
∵MG?平面BCEF,∴DM⊥MG,
∵梯形BFEC中,EC=FG=BG=1,BF∥EC,∴四边形EFGC是平行四边形,可得EF∥CG
∵EF⊥平面ABF,∴CG⊥平面ABF,可得CG⊥BG
Rt△BCG中,BG=1,BC=
| 2 |
| BC2-BG2 |
∴Rt△GCM中,GM=
| GC2+CM2 |
| ||
| 2 |
又∵DM=
| ||
| 2 |
| ||
| 2 |
∴Rt△GDM中,DG=
| GM2+DM2 |
| 2 |
点评:本题以一个平面翻折问题为载体,证明了线面垂直并且求出了两点之间的距离,着重考查了空间平行、垂直位置关系的证明和距离计算等知识,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 (2012•河北模拟)设全集U=R,A={x|
(2012•河北模拟)设全集U=R,A={x| (2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是
(2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是 (2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )
(2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )