题目内容
（2012•河北模拟）设全集U=R，A={x|2(x-1)2＜2}，B={x|log| 1 |
| 2 |
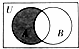
分析：先分别化简集合A，B，利用图中阴影部分表示的集合为A∩CUB，可得结论．
解答：解：由题意，∵2(x-1)2＜2，∴（x-1）2＜1，∴0＜x＜2，∴A=（0，2）
∵log
(x2+x+1)＞-log2(x2+2)
∴x2+x+1＜x2+2，
∴x＜1
∴CUB=[1，+∞）
图中阴影部分表示的集合为A∩CUB=[1，2）
故选A．
∵log
| 1 |
| 2 |
∴x2+x+1＜x2+2，
∴x＜1
∴CUB=[1，+∞）
图中阴影部分表示的集合为A∩CUB=[1，2）
故选A．
点评：本题考查解不等式，考查集合的运算，正确化简集合是关键．
练习册系列答案
相关题目
（2012•河北模拟）如图是一个程序框图，该程序框图输出的结果是
（2012•河北模拟）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其导函数f'（x）的部分图象如图所示，则函数f（x）的解析式为（ ）