题目内容
(2012•河北模拟)已知函数f(x)=xlnx,g(x)=-x2+ax-2
(Ⅰ)求函数f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)若函数y=f(x)+g(x)有两个不同的极值点x1,x2(x1<x2)且x2-x1>ln2,求实数a的取值范围.
(Ⅰ)求函数f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)若函数y=f(x)+g(x)有两个不同的极值点x1,x2(x1<x2)且x2-x1>ln2,求实数a的取值范围.
分析:(I)求导数,再分类讨论,确定函数在区间上的单调性,即可求得函数的最小值;
(II)函数由两个不同的极值点转化为导函数等于0的方程有两个不同的实数根,进而转化为图象的交点问题,由此可得结论.
(II)函数由两个不同的极值点转化为导函数等于0的方程有两个不同的实数根,进而转化为图象的交点问题,由此可得结论.
解答:解:(I)由f′(x)=lnx+1=0,可得x=
,
∴∴①0<t<
,时,函数f(x)在(t,
)上单调递减,在(
,t+2)上单调递增,
∴函数f(x)在[t,t+2](t>0)上的最小值为f(
)=-
,
②当t≥
时,f(x)在[t,t+2]上单调递增,
∴f(x)min=f(t)=tlnt,
∴f(x)min=
;
(II)y=f(x)+g(x)=xlnx-x2+ax-2,则y′=lnx-2x+1+a
题意即为y′=lnx-2x+1+a=0有两个不同的实根x1,x2(x1<x2),
即a=-lnx+2x-1有两个不同的实根x1,x2(x1<x2),
等价于直线y=a与函数G(x)=-lnx+2x-1的图象有两个不同的交点
∵G′(x)=-
+2,∴G(x)在(0,
)上单调递减,在(
,+∞)上单调递增,
画出函数图象的大致形状(如右图),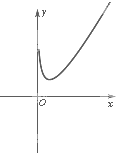
由图象知,当a>G(x)min=G(
))=ln2时,x1,x2存在,且x2-x1的值随着a的增大而增大而当x2-x1=ln2时,由题意
,
两式相减可得ln
=2(x1-x2)=-2ln2
∴x2=4x1代入上述方程可得x2=4x1=
ln2,
此时a=
ln2-ln(
)-1,
所以,实数a的取值范围为a>
ln2-ln(
)-1;
| 1 |
| e |
∴∴①0<t<
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
∴函数f(x)在[t,t+2](t>0)上的最小值为f(
| 1 |
| e |
| 1 |
| e |
②当t≥
| 1 |
| e |
∴f(x)min=f(t)=tlnt,
∴f(x)min=
|
(II)y=f(x)+g(x)=xlnx-x2+ax-2,则y′=lnx-2x+1+a
题意即为y′=lnx-2x+1+a=0有两个不同的实根x1,x2(x1<x2),
即a=-lnx+2x-1有两个不同的实根x1,x2(x1<x2),
等价于直线y=a与函数G(x)=-lnx+2x-1的图象有两个不同的交点
∵G′(x)=-
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
画出函数图象的大致形状(如右图),

由图象知,当a>G(x)min=G(
| 1 |
| 2 |
|
两式相减可得ln
| x1 |
| x2 |
∴x2=4x1代入上述方程可得x2=4x1=
| 4 |
| 3 |
此时a=
| 2 |
| 3 |
| ln2 |
| 3 |
所以,实数a的取值范围为a>
| 2 |
| 3 |
| ln2 |
| 3 |
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查的知识点比较多,考查数形结合的数学思想,综合性强.

练习册系列答案
相关题目
 (2012•河北模拟)设全集U=R,A={x|
(2012•河北模拟)设全集U=R,A={x| (2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是
(2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是 (2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )
(2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )