题目内容
已知函数y=f(x)是定义在R上的减函数,函数y=f(x-1)的图象关于点 (1,0)对称.若对任意的x,y∈R,不等式 f(x2+y-1)+f(-x2+2x-1)≤0恒成立,4x2+y2的最小值是( )A.0
B.1
C.2
D.3
【答案】分析:根据函数y=f(x-1)的图象关于点 (1,0)对称,可得函数是奇函数,利用函数y=f(x)是定义在R上的减函数,可得y≥-2x+2,设t=4x2+y2,利用换元法,即可求4x2+y2的最小值.
解答:解:∵函数y=f(x-1)的图象关于点 (1,0)对称,
∴函数y=f(x)的图象关于点 (0,0)对称,即函数是奇函数
∴不等式f(x2+y-1)+f(-x2+2x-1)≤0等价于不等式f(x2+y-1)≤f(x2-2x+1)
∵函数y=f(x)是定义在R上的减函数,
∴x2+y-1≥x2-2x+1,∴y≥-2x+2
设t=4x2+y2,则x=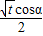 ,y=
,y=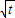 sinα,∴
sinα,∴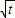 sinα≥-
sinα≥-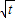 cosα+2
cosα+2
∴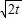 sin(α+
sin(α+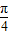 )≥2
)≥2
∴ ≥2,∴t≥2
≥2,∴t≥2
即4x2+y2的最小值是2
故选C.
点评:本题考查函数的奇偶性,考查函数的最值,考查解不等式,考查学生分析解决问题的能力,属于中档题.
解答:解:∵函数y=f(x-1)的图象关于点 (1,0)对称,
∴函数y=f(x)的图象关于点 (0,0)对称,即函数是奇函数
∴不等式f(x2+y-1)+f(-x2+2x-1)≤0等价于不等式f(x2+y-1)≤f(x2-2x+1)
∵函数y=f(x)是定义在R上的减函数,
∴x2+y-1≥x2-2x+1,∴y≥-2x+2
设t=4x2+y2,则x=
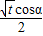 ,y=
,y=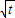 sinα,∴
sinα,∴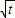 sinα≥-
sinα≥-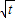 cosα+2
cosα+2∴
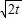 sin(α+
sin(α+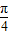 )≥2
)≥2∴
 ≥2,∴t≥2
≥2,∴t≥2即4x2+y2的最小值是2
故选C.
点评:本题考查函数的奇偶性,考查函数的最值,考查解不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足