题目内容
17.已知函数f(x)=2sin(2x+$\frac{π}{3}}$)+1.(1)求函数f(x)的最大值,并求取得最大值时x的值;
(2)求函数f(x)的单调递增区间.
分析 (1)由条件利用正弦函数的最值求得函数f(x)的最大值,并求取得最大值时x的值.
(2)由条件利用正弦函数的单调性求得函数f(x)的单调递增区间.
解答 解:(1)对于函数f(x)=2sin(2x+$\frac{π}{3}}$)+1,当2x+$\frac{π}{3}}$=2kπ+$\frac{π}{2}$,即x=kπ+$\frac{π}{12}$,k∈z时,
f(x)取得最大值为3.
(2)令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}}$≤2kπ+$\frac{π}{2}$,即kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$ 时,函数f(x)为增函数,
故函数f(x)的递增区间是[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈z.
点评 本题主要考查正弦函数的最值和单调性,属于基础题.

练习册系列答案
相关题目
8.在△ABC中,$c=\sqrt{2}$,acosC=csinA,若当a=x0时的△ABC有两解,则x0的取值范围是( )
| A. | $(1,\sqrt{2})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},2)$ | D. | $(\sqrt{2},2)$ |
12.执行如图的程序框图,若输入m的值为2,则输出的结果i=( )
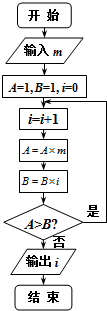

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
6.设正实数x,y,z满足x2-7xy+16y2-z=0,则当$\frac{z}{xy}$取得最小值时,x+2y-z的最大值为( )
| A. | 0 | B. | $\frac{9}{8}$ | C. | $\frac{9}{4}$ | D. | 2 |