题目内容
如右图所示，一个空间几何体的主视图和左视图都是边长为
的正方形，俯视图是一个直径为的圆，那么这个几何体的全面积为（ ）
A．
B．
C．
D． 
D
【解析】
试题分析：由三视图分析可知此几何体为圆柱，底面半径为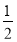
，高为1，所以此几何体全面积为
。故D正确。
考点：1三视图；2圆柱的表面积。
练习册系列答案
相关题目
题目内容
如右图所示，一个空间几何体的主视图和左视图都是边长为的正方形，俯视图是一个直径为的圆，那么这个几何体的全面积为（ ）
A． B． C． D．
D
【解析】
试题分析：由三视图分析可知此几何体为圆柱，底面半径为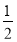，高为1，所以此几何体全面积为。故D正确。
考点：1三视图；2圆柱的表面积。
