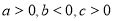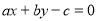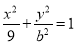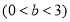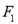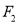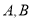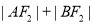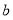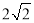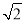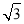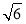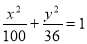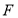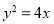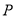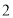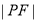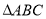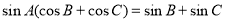题目内容
已知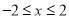 ,
,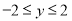 ,点
,点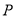 的坐标为
的坐标为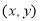 .
.
(1)求当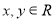 时,点
时,点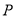 满足
满足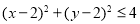 的概率;
的概率;
(2)求当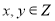 时,点
时,点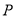 满足
满足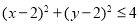 的概率.
的概率.
(1)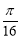 ;(2)
;(2)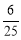 .
.
【解析】
试题分析:(1)这是几何概型的概率计算问题,先确定总区域即不等式组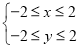 所表示的平面区域的面积
所表示的平面区域的面积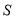 ,后确定不等式组
,后确定不等式组 所表示的平面区域的面积
所表示的平面区域的面积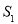 ,最后根据几何概型的概率计算公式
,最后根据几何概型的概率计算公式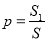 计算即可;(2)先计算出满足不等式组
计算即可;(2)先计算出满足不等式组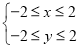 所包含的整点的个数
所包含的整点的个数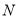 ,后确定不等式组
,后确定不等式组 所包含的整点的个数
所包含的整点的个数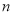 ,最后由
,最后由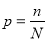 即可得到所求的概率.
即可得到所求的概率.
试题解析:(1)点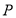 所在的区域为正方形
所在的区域为正方形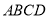 的内部(含边界) (1分)
的内部(含边界) (1分)
满足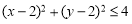 的点的区域为以
的点的区域为以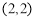 为圆心,2为半径的圆面(含边界) (3分)
为圆心,2为半径的圆面(含边界) (3分)
 所求的概率
所求的概率 (5分)
(5分)
(2)满足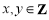 ,且
,且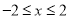 ,
,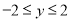 的整点有25个 (8分)
的整点有25个 (8分)
满足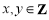 ,且
,且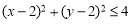 的整点有6个 (11分)
的整点有6个 (11分)
 所求的概率
所求的概率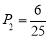 (12分).
(12分).
考点:1.古典概率;2.几何概型的概率.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目