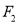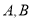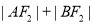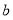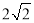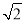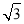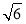题目内容
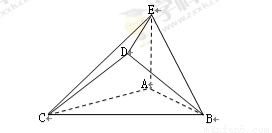
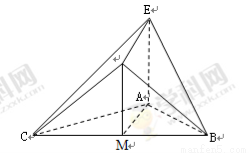
在如图所示的几何体中,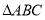 是边长为
是边长为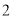 的正三角形,
的正三角形,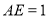 ,
,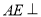 平面
平面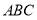 ,平面
,平面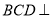 平面
平面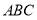 ,
,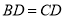 ,且
,且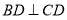 .
.
(1)证明: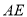 //平面
//平面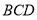 ;
;
(2)证明:平面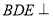 平面
平面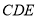 ;
;
(3)求该几何体的体积.
(1)详见解析;(2)详见解析;(3)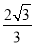
【解析】
试题分析:(1)取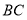 的中点
的中点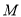 ,根据等腰三角形中线即为高线可得
,根据等腰三角形中线即为高线可得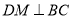 ,又因为面
,又因为面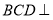 平面
平面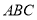 ,根据面面垂直的性质定理可得
,根据面面垂直的性质定理可得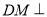 平面
平面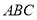 ,已知
,已知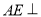 平面
平面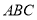 ,所以
,所以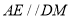 ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得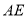 //平面
//平面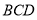 。(2)因为
。(2)因为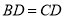 ,且
,且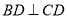 ,斜边中线
,斜边中线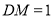 ,又因为
,又因为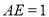 ,
,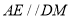 可证得
可证得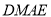 是平行四边形,可得
是平行四边形,可得 ,根据线面垂直的判定定理可证得
,根据线面垂直的判定定理可证得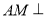 平面
平面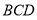 ,即
,即 平面
平面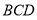 ,从而可得
,从而可得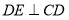 ,又因为
,又因为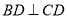 即可证得
即可证得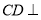 平面
平面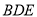 ,从而证得平面
,从而证得平面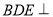 平面
平面 。(3)根据前两问的条件可证得
。(3)根据前两问的条件可证得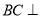 平面
平面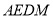 ,从而可将此几何体分割为以四边形
,从而可将此几何体分割为以四边形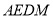 为底面的两个四棱锥,然后再求其体积。
为底面的两个四棱锥,然后再求其体积。
试题解析:证明:
(1) 取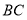 的中点
的中点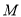 ,连接
,连接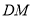 、
、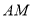 ,
,
由已知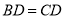 ,可得:
,可得: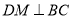 ,
,
又因为平面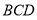 ⊥平面
⊥平面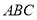 ,平面
,平面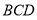
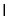 平面
平面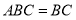 ,
,
所以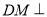 平面
平面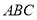 ,
,
因为 平面
平面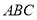 , 所以
, 所以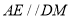 ,
,
又因为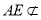 平面
平面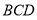 ,
,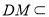 平面
平面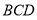 ,
,
所以 平面
平面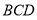 . 4分
. 4分
(2)由(1)知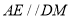 ,又
,又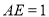 ,
,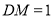 ,
,
所以四边形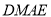 是平行四边形,则有
是平行四边形,则有 ,
,
由(1)得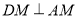 ,又
,又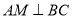 ,
,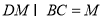

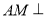 平面
平面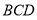 , 所以
, 所以 平面
平面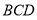 ,
,
又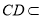 平面
平面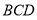 ,所以
,所以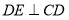 ,
,
由已知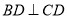 ,
, 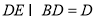 ,
,
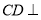 平面
平面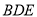 ,
,
因为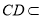 平面
平面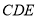 , 所以平面
, 所以平面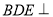 平面
平面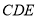 . 10分
. 10分
(也可利用勾股定理等证明题中的垂直关系)
(3)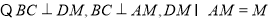 ,
,
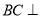 平面
平面 , 11分
, 11分
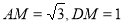 ,易得四边形
,易得四边形 为矩形其面积
为矩形其面积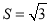 , 12分
, 12分
故该几何体的体积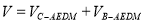 =
=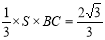 . 14分
. 14分
考点:1线面平行;2面面垂直;3棱锥的体积。

练习册系列答案
相关题目