题目内容
【题目】直线l与两直线y=1,x﹣y﹣7=0分别交于A,B两点,若直线AB的中点是M(1,﹣1),则直线l的斜率为 .
【答案】![]()
【解析】解:设直线l的斜率为k,又直线l过M(1,﹣1),则直线l的方程为y+1=k(x﹣1),联立直线l与y=1,得到 ![]() ,
,
解得x= ![]() ,
,
∴A( ![]() ,1);
,1);
联立直线l与x﹣y﹣7=0,得到 ![]() ,
,
解得x= ![]() ,y=
,y= ![]() ,
,
∴B( ![]() ,
, ![]() ),
),
又线段AB的中点M(1,﹣1),
∴ 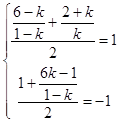 ,解得k=﹣
,解得k=﹣ ![]() .
.
所以答案是: ![]()
【考点精析】根据题目的已知条件,利用直线的斜率的相关知识可以得到问题的答案,需要掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα.

练习册系列答案
相关题目
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次 射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.

