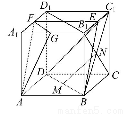
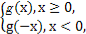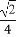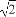题目内容

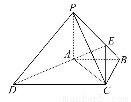
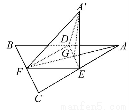
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,

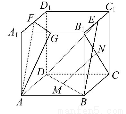
求证:(1)MN∥平面CDD1C1.

(2)平面EBD∥平面FGA.

 

见解析

【解析】证明:(1)连接BC1,DC1,

∵四边形BCC1B1为正方形,N为B1C的中点,

∴N在BC1上,且N为BC1的中点.

又∵M为BD的中点,∴MN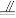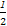DC1.

又MN?平面CDD1C1,DC1?平面CDD1C1,

∴MN∥平面CDD1C1.

(2)连接EF,B1D1,则EF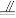AB.

∴四边形ABEF为平行四边形,∴AF∥BE.

又易知FG∥B1D1,B1D1∥BD,∴FG∥BD.

又∵AF∩FG=F,BE∩BD=B,

∴平面EBD∥平面FGA.

 

练习册系列答案
相关题目

已知函数g(x)=2x-,若f(x)=则函数f(x)在定义域内(　　)

(A)有最小值,但无最大值

(B)有最大值,但无最小值

(C)既有最大值,又有最小值

(D)既无最大值,又无最小值

 

如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.

(1)若PD∥平面EAC,试确定点E在棱PB上的位置.

(2)在(1)的条件下,求二面角A-CE-P的余弦值.

 

已知l∥α,且l的方向向量为u=(2,m,1),平面α的法向量为v=(1,,2),则m=　　　　　.

 

设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k等于(　　)

(A)2 (B)-4 (C)4 (D)-2

 

如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形(A'不与A,F重合),则下列命题中正确的是(　　)

①动点A'在平面ABC上的射影在线段AF上;

②BC∥平面A'DE;③三棱锥A'-FED的体积有最大值.

(A)① (B)①② (C)①②③ (D)②③

 

一个水平放置的平面图形的斜二测直观图是直角梯形 (如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )

(A)+ (B)2+

(C)+ (D)+

 

正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角等于　　　.

 

已知向量a=(1,-1,1),b=(-1,2,1),且ka-b与a-3b互相垂直,则k的值是(　　)

(A)1 (B) (C) (D)-

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网