��Ŀ����
 ��֪��Բ
��֪��Բ| x2 |
| a2 |
| y2 |
| b2 |
��1������Բ�ķ��̣�
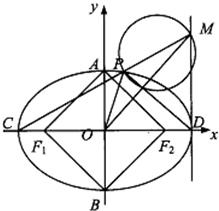
��2����C��D�ֱ�����Բ�������Ҷ˵㣬����M����MD��CD������CM������Բ�ڵ�P��֤����
| OM |
| OP |
��3���ڣ�2���������£�����x�����Ƿ�����ڵ�C�Ķ���Q��ʹ����MPΪֱ����Բ���ֱ��DP��MQ�Ľ��㣬�����ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��������1��������֪a=2��b=c��b2=2���ɴ˿�֪��Բ����Ϊ
+
=1��
��2����M��2��y0����P��x1��y1������
=(x1��y1)��
=(2��y0)��ֱ��CM��y=
(x+2)����y=
x+
y0��������Բ����x2+2y2=4����(1+
)x2+
x+
-4=0��Ȼ�����ø���ϵ���Ĺ�ϵ�ܹ��Ƶ���
•
Ϊ��ֵ��
��3�������Q��m��0��������������MQ��DP��
=(m-2��-y0)��
=(-
��
)������
•
=0��-
(m-2)-
=0���ɴ˿�֪����Q��0��0������������
| x2 |
| 4 |
| y2 |
| 2 |
��2����M��2��y0����P��x1��y1������
| OP |
| OM |
| y0 |
| 4 |
| y0 |
| 4 |
| 1 |
| 2 |
| ||
| 8 |
| 1 |
| 2 |
| y | 2 0 |
| 1 |
| 2 |
| y | 2 0 |
| OM |
| OP |
��3�������Q��m��0��������������MQ��DP��
| MQ |
| DP |
4
| ||
|
| 8y0 | ||
|
| MQ |
| DP |
4
| ||
|
8
| ||
|
����⣺��1��a=2��b=c��a2=b2+c2����b2=2��
����Բ����Ϊ
+
=1��4�֣�
��2��C��-2��0����D��2��0������M��2��y0����P��x1��y1����
��
=(x1��y1)��
=(2��y0)
ֱ��CM��y=
(x+2)����y=
x+
y0��������Բ����x2+2y2=4��
��(1+
)x2+
x+
-4=0��6�֣�
��x1=-
����x1=-
����y1=
����
=(-
��
)��8�֣�
��
•
=-
+
=
=4����ֵ����10�֣�
��3�������Q��m��0��������������MQ��DP��11�֣�
=(m-2��-y0)��
=(-
��
)��12�֣�
����
•
=0��-
(m-2)-
=0���Ӷ���m=0
�����Q��0��0������������14�֣�
����Բ����Ϊ
| x2 |
| 4 |
| y2 |
| 2 |
��2��C��-2��0����D��2��0������M��2��y0����P��x1��y1����
��
| OP |
| OM |
ֱ��CM��y=
| y0 |
| 4 |
| y0 |
| 4 |
| 1 |
| 2 |
��(1+
| ||
| 8 |
| 1 |
| 2 |
| y | 2 0 |
| 1 |
| 2 |
| y | 2 0 |
��x1=-
| 1 |
| 2 |
4(
| ||
|
2(
| ||
|
| 8y0 | ||
|
| OP |
2(
| ||
|
| 8y0 | ||
|
��
| OP |
| OM |
4(
| ||
|
8
| ||
|
4
| ||
|
��3�������Q��m��0��������������MQ��DP��11�֣�
| MQ |
| DP |
4
| ||
|
| 8y0 | ||
|
����
| MQ |
| DP |
4
| ||
|
8
| ||
|
�����Q��0��0������������14�֣�
���������⿼��ֱ�ߺ���Բ��λ�ù�ϵ������ʱҪ�������⣬��ϸ���

��ϰ��ϵ�д�
�����Ŀ