题目内容
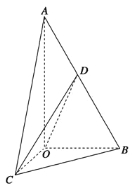
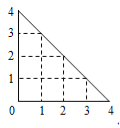
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获![]() (单位:
(单位:![]() )与它的“相近”作物株数
)与它的“相近”作物株数![]() 之间的关系如下表所示:
之间的关系如下表所示:
| 1 | 2 | 3 | 4 |
| 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)在所种作物中堆积选取一株,求它的年收获量的分布列与数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)三角形地块内部的作物为![]() ,边界上的作物为
,边界上的作物为![]() ,所以分别随机选取一株的不同结果数为
,所以分别随机选取一株的不同结果数为![]() ,与
,与![]() 相近的有
相近的有![]() ,与
,与![]() 相近的有
相近的有![]() ,与
,与![]() 相近的有
相近的有![]() ,因此两株作物恰好相近的不同结果数有
,因此两株作物恰好相近的不同结果数有![]() ,故概率为
,故概率为![]()
![]() ;(2)所选作物中相近作物株数为
;(2)所选作物中相近作物株数为![]() 的有
的有![]() ,相近株数为
,相近株数为![]() 的有
的有![]() ,相近株数为
,相近株数为![]() 的有
的有![]() ,其余的为相近株数为
,其余的为相近株数为![]() 的作物,根据古典概型求出概率和期望.
的作物,根据古典概型求出概率和期望.
试题解析:解:(1)所种作物总株数![]() ,其中三角形地块内部的作物株数为3,边界上的作物株数为12,从三角形地块的内部和边界上分别随机选取一株的不同结果有
,其中三角形地块内部的作物株数为3,边界上的作物株数为12,从三角形地块的内部和边界上分别随机选取一株的不同结果有![]() 种,选取的两株作物恰好“相近”的不同结果有
种,选取的两株作物恰好“相近”的不同结果有![]() ,
,
所以从三角形地块的内部和边界上分别随机选取一株作物,则它们恰好“相近”的概率为![]() .
.
(2)先求从所种作物中随机选取一株作物的年收获量为![]() 的分布列,
的分布列,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴只需求出![]() (
(![]() )即可,记
)即可,记![]() 为其“相近”作物恰有
为其“相近”作物恰有![]() 株的作物株数(
株的作物株数(![]() ),则
),则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
, ![]() ,
,![]() ,
,![]() .
.
所以所求的分布列为:
| 51 | 48 | 45 | 42 |
|
|
|
|
|
数学期望为![]() .
.

【题目】一对父子参加一个亲子摸奖游戏,其规则如下:父亲在装有红色、白色球各两个的甲袋子里随机取两个球,儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球,父子俩取球互相独立,两人各摸球一次合在一起称为一次摸奖,他们取出的三个球的颜色情况与他们获得的积分对应如下表:
所取球的情况 | 三个球均为红色 | 三个球均为不同色 | 恰有两球为红色 | 其他情况 |
所获得的积分 | 180 | 90 | 60 | 0 |
(1)求一次摸奖中,所取的三个球中恰有两个是红球的概率;
(2)设一次摸奖中,他们所获得的积分为![]() ,求
,求![]() 的分布列及均值(数学期望)
的分布列及均值(数学期望)![]() ;
;
(3)按照以上规则重复摸奖三次,求至少有两次获得积分为60的概率.