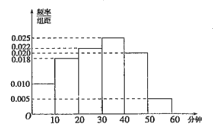
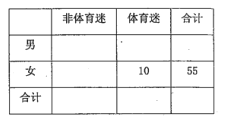
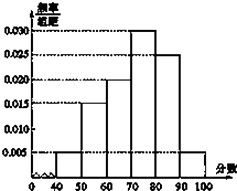
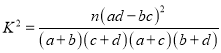题目内容
【题目】已知函数![]() (
(![]() 且
且![]() ,
, ![]() 为自然对数的底数).
为自然对数的底数).
(1)若曲线![]() 在点
在点![]() 处的切线斜率为0,且
处的切线斜率为0,且![]() 有极小值,
有极小值,
求实数![]() 的取值范围.
的取值范围.
(2)当 ![]() 时,若不等式:
时,若不等式: ![]() 在区间
在区间![]() 内恒成立,求实数
内恒成立,求实数![]() 的最大值.
的最大值.
【答案】(Ⅰ)(﹣∞,0); (Ⅱ)1+e
【解析】试题分析:
(1)首先求解导函数,结合导函数与原函数的关系可得实数a的取值范围为(﹣∞,0);
(2)不等式等价于xf(x)﹣m(x﹣1)>e,构造新函数h(x)=lnx+ex﹣m(x﹣1) ,结合题意讨论新函数的性质可得实数![]() 的最大值为1+e.
的最大值为1+e.
试题解析:
(Ⅰ)![]()
![]() ,
, ![]()
∵f′(e)=0,∴b=0,则![]()
当a>0时,f′(x)在(0,e)内大于0,在(e,+∞)内小于0,
∴f(x)在(0,e)内为增函数,在(e,+∞)内为减函数,即f(x)有极大值而无极小值;
当a<0时,f(x)在(0,e)内为减函数,在(e,+∞)内为增函数,
即f(x)有极小值而无极大值.
∴a<0,即实数a的取值范围为(﹣∞,0);
(Ⅱ)xf(x)>e+m(x﹣1)![]() xf(x)﹣m(x﹣1)>e,
xf(x)﹣m(x﹣1)>e,
当 a=1,b=﹣1 时,设h(x)=xf(x)﹣m(x﹣1)=lnx+ex﹣m(x﹣1).
则h′(x)= ![]() .
.
令t(x)=h′(x)= ![]() .
.
∵x>1,∴t′(x)= ![]() .
.
∴h′(x)在(1,+∞)内单调递增,
∴当x>1时,h′(x)>h′(1)=1+e﹣m.
①当1+e﹣m≥0时,即m≤1+e时,h′(x)>0,
∴h(x)在区间(1,+∞)内单调递增,
∴当x>1时,h(x)>h(1)=e恒成立;
②当1+e﹣m<0时,即m>1+e时,h′(x)<0,
∴存在x0∈(1,+∞),使得h′(x0)=0.∴h(x)在区间(1,x0)内单调递减,
在(x0 , +∞)内单调递增.由h(x0)<h(1)=e,
∴h(x)>e不恒成立.综上所述,实数m的取值范围为(﹣∞,1+e].
∴实数m的最大值为:1+e.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案