题目内容
在墙上挂着一块边长为16cm的正方形木板,上面画了大、中、小三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m之外向此板投镖,设投中线上或没有投中木板时不算,可重投,问:
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
S正方形=162="256" Cm2,S大圆=π×6=36πCm2,S大圆外=(256-36π) Cm2.
则(1)投中大圆内的概率P(A1)=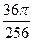 =
= .
.
(2)投中小圆与中圆形成的圆环的概率P(A2)= =
=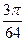 .
.
(3)投中大圆之外的概率P(A3)=1-P(A1)=1-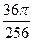 =1-
=1- .
.
则(1)投中大圆内的概率P(A1)=
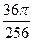 =
= .
.(2)投中小圆与中圆形成的圆环的概率P(A2)=
 =
=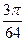 .
.(3)投中大圆之外的概率P(A3)=1-P(A1)=1-
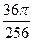 =1-
=1- .
.本题满足投到各位置的可能性相等,而落点具有无限个,因此是与面积相关的几何概型.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
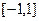 上任取两数
上任取两数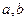 ,运用随机模拟方法求二次方程
,运用随机模拟方法求二次方程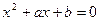 两根均为正数的概率。
两根均为正数的概率。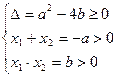
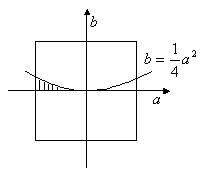



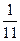
 和
和 ,则
,则 的概率为
的概率为


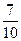 .
.