题目内容
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.

(1)求 ·
· +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin  的值.
的值.
(1)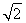 +1(2)
+1(2)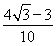
【解析】(1)由已知,得A(1,0),B(0,1),P(cos θ,sin θ),
因为四边形OAQP是平行四边形,
所以 =
= +
+ =(1,0)+(cos θ,sin θ)
=(1,0)+(cos θ,sin θ)
=(1+cos θ,sin θ).
所以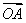 ·
· =1+cos θ.
=1+cos θ.
又平行四边形OAQP的面积为
S=| |·|
|·|  |sin θ=sin θ,
|sin θ=sin θ,
所以 ·
·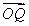 +S=1+cos θ+sin θ=
+S=1+cos θ+sin θ= sin
sin  +1.
+1.
又0<θ<π,
所以当θ= 时,
时, ·
· +S的最大值为
+S的最大值为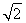 +1.
+1.
(2)由题意,知 =(2,1),
=(2,1), =(cos θ,sin θ),
=(cos θ,sin θ),
因为CB∥OP,所以cos θ=2sin θ.
又0<θ<π,cos2θ+sin2θ=1,
解得sin θ= ,cos θ=
,cos θ= ,
,
所以sin2 θ=2sin θcos θ= ,cos2θ=cos2θ-sin2θ=
,cos2θ=cos2θ-sin2θ= .
.
所以sin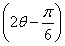 =sin 2θcos
=sin 2θcos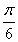 -cos 2θsin
-cos 2θsin =
= ×
× -
- ×
× =
= .
.

练习册系列答案
相关题目

















