Question

已知二次函数f(x)的二次项系数为a，且不等式f(x)＞2x的解集为(－1,3)．

(1)若函数g(x)＝xf(x)在区间内单调递减，求a的取值范围；

(2)当a＝－1时，证明方程f(x)＝2x3－1仅有一个实数根；

(3)当x∈[0,1]时，试讨论|f(x)＋(2a－1)x＋3a＋1|≤3成立的充要条件．

 

Answer 1

（1）(－∞，－1]（2）见解析（3）－5≤a＜0

【解析】(1)∵f(x)－2x＞0的解集为(－1,3)，

∴可设f(x)－2x＝a(x＋1)(x－3)，且a＜0，

因而f(x)＝a(x＋1)(x－3)＋2x＝ax2＋2(1－a)x－3a①

g(x)＝xf(x)＝ax3＋2(1－a)x2－3ax，

∵g(x)在区间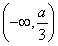内单调递减，

∴g′(x)＝3ax2＋4(1－a)x－3a在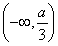上的函数值非正，

由于a＜0，对称轴x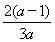＝＞0，故只需g′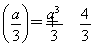a(1－a)－3a≤0，注意到a＜0，∴a2＋4(1－a)－9≥0，得a≤－1或a≥5(舍去)．

故所求a的取值范围是(－∞，－1]．

(2)a＝－1时，方程f(x)＝2x3－1仅有一个实数根，即证方程2x3＋x2－4x－4＝0仅有一个实数根．令h(x)＝2x3＋x2－4x－4，由h′(x)＝6x2＋2x－4＝0，得x1＝－1，x2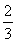＝，易知h(x)在(－∞，－1)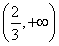，上递增，在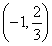上递减，h(x)的极大值h(－1)＝－1＜0，故函数h(x)的图象与x轴仅有一个交点，∴a＝－1时，方程f(x)＝2x3－1仅有一个实数根，得证．

(3)设r(x)＝f(x)＋(2a－1)x＋3a＋1＝ax2＋x＋1，r(0)＝1，对称轴为x＝－，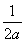

由题意，得或

解出－5≤a＜0，

故使|f(x)＋(2a－1)x＋3a＋1|≤3成立的充要条件是－5≤a＜0