Question

已知数列{an}的前n项和为Sn，且满足Sn＝n2，数列{bn}满足bn＝，Tn为数列{bn}的前n项和．

(1)求数列{an}的通项公式an和Tn；

(2)若对任意的n∈N*，不等式λTn<n＋(－1)n恒成立，求实数λ的取值范围．

 

Answer 1

（1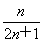）（2）(－∞，0)

【解析】(1)当n＝1时，a1＝S1＝1，当n≥2时，an＝Sn－Sn－1＝2n－1，验证当n＝1时，也成立；所以an＝2n－1.

bn＝＝，

所以Tn＝.

(2)由(1)得λ<，

当n为奇数时，λ<＝2n－－1恒成立，

因为当n为奇数时，2n－－1单调递增，

所以当n＝1时，2n－－1取得最小值为0，

此时，λ<0.

当n为偶数时，λ<＝2n＋＋3恒成立，

因为当n为偶数时，2n＋＋3单调递增，

所以当n＝2时，2n＋＋3取得最小值为.

此时，λ<.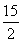

综上所述，对于任意的正整数n，原不等式恒成立，λ的取值范围是(－∞，0)