题目内容
已知f(x),g(x)都是定义在R上的函数,且f(x)=g(x)ax(a>0且a≠1),f′(x)g(x)<f(x)g′(x),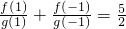 ,则a的值为________.
,则a的值为________.

分析:先根据
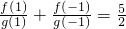 得到含a的式子,求出a的两个值,再由已知,利用导数判断函数
得到含a的式子,求出a的两个值,再由已知,利用导数判断函数 =ax的单调性,求出a的范围,判断a的两个之中哪个成立即可.
=ax的单调性,求出a的范围,判断a的两个之中哪个成立即可.解答:令x=1,由f(x)=g(x)ax(a>0且a≠1),得到f(1)=a•g(1).
令x=-1,f(-1)=
 ,
,分别代入
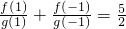 得:a+
得:a+ =
= ,化简得2a2-5a+2=0,
,化简得2a2-5a+2=0,即(2a-1)(a-2)=0,解得a=2或a=
 .
.又由f(x)•g'(x)>f'(x)•g(x),即f(x)g'(x)-f'(x)g(x)>0,也就是
 =
=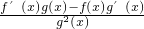 <0,说明函数
<0,说明函数 =ax是减函数,
=ax是减函数,故有0<a<1,故只有a=
 ,
,故答案为
 .
.点评:此题考查学生会利用有理数指数幂公式化简求值,应用导数判断函数的单调性,是一道基础题.

练习册系列答案
相关题目