题目内容
已知函数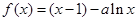
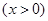 .
.
(1)求函数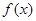 的单调区间和极值;
的单调区间和极值;
(2)若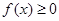 对
对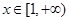 上恒成立,求实数
上恒成立,求实数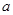 的取值范围.
的取值范围.
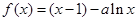
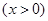 .
.(1)求函数
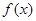 的单调区间和极值;
的单调区间和极值;(2)若
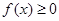 对
对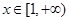 上恒成立,求实数
上恒成立,求实数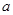 的取值范围.
的取值范围.(1)e;(2)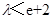
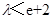
试题分析:(1)先求导函数
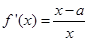 ,然后利用导数求极值的方法和对a进行分类讨论解决问题;(2)对a分
,然后利用导数求极值的方法和对a进行分类讨论解决问题;(2)对a分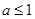 和
和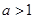 利用导数分析单调性进行分类讨论即可.
利用导数分析单调性进行分类讨论即可.试题解析:(1)
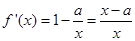
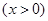 ,
,当
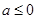 时,
时,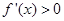 ,在
,在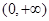 上增,无极值;
上增,无极值;当
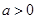 时,
时,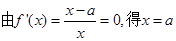 ,
,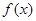 在
在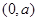 上减,在
上减,在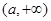 上增,
上增,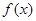 有极小值
有极小值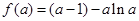 ,无极大值; 6分
,无极大值; 6分(2)
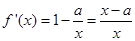 ,
,当
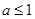 时,
时,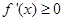 在
在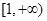 上恒成立,则
上恒成立,则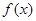 是单调递增的,
是单调递增的,则只需
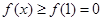 恒成立,所以
恒成立,所以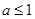 ,
,当
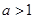 时,
时,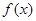 在上
在上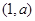 减,在
减,在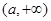 上单调递增,所以当
上单调递增,所以当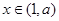 时,
时,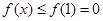 这与
这与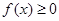 恒成立矛盾,故不成立,综上:
恒成立矛盾,故不成立,综上: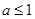 . 13分
. 13分
练习册系列答案
相关题目
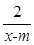 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若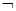 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围. ,若函数
,若函数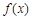 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数 的取值范围.
的取值范围.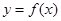 对任意的
对任意的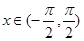 满足
满足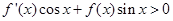 (其中
(其中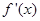 是函数
是函数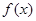 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )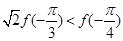
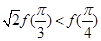
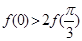
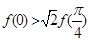
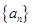 是首项为
是首项为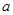 ,公差为1的等差数列,
,公差为1的等差数列,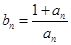 ,若对任意的
,若对任意的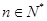 ,都有
,都有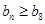 成立,则实数
成立,则实数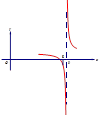
 在
在 上为偶函数,当
上为偶函数,当 时,
时,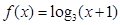 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是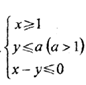 ,若函数z=x+y的最大值为4,则实数a的值为( )
,若函数z=x+y的最大值为4,则实数a的值为( )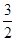
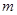 对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在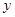 轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与
轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与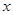 轴交于点N(
轴交于点N(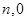 ),则
),则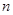 ,记作
,记作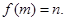

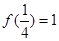 ; ②
; ②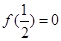 ; ③
; ③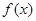 是奇函数; ④
是奇函数; ④