题目内容
复平面上两点A、B分别对应复数-3和z,其中|z|=1,线段AB靠近A点的三等分点为P.(1)求P点的轨迹方程;
(2)若向量![]() 对应复数为z′,求z′所对应的点的轨迹方程.
对应复数为z′,求z′所对应的点的轨迹方程.
思路分析:借助定比分点坐标公式,找出点P与A、B间的关系,然后将B点坐标用点P坐标表示,代入方程|z|=1中.
解:(1)设P(x,y)、B(x′,y′).
∵|z|=1,∴x′2+y′2=1,
知点P分![]() 的比λ=2.
的比λ=2.
由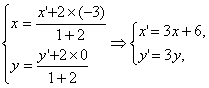
则(3x+6)2+(3y)2=1,∴点P的轨迹方程为(x+2)2+y2=![]() .
.
(2)设B(x′,y′),则x′2+y′2=1,
则![]() 的对应复数为x′+y′i.
的对应复数为x′+y′i.
由![]() +
+![]() =
=![]() ,知
,知![]() =
=![]() -
-![]() ,
,
∴向量![]() 对应复数为
对应复数为
x′+y′i-(-3)=x′+y′i=3.
由![]() =3
=3![]() ,
,
则![]() 对应复数为z′=
对应复数为z′=![]() i.
i.
设z′的对应点为M(x,y),
则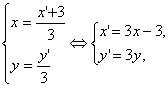
∴(3x-3)2+(3y)2=1.
∴z′对应点的轨迹方程为(x-1)2+y2=![]() .
.

练习册系列答案
相关题目
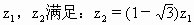 ,且
,且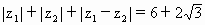 ,点O是复平面的坐标原点.
,点O是复平面的坐标原点.