题目内容
从120°二面角的棱上两点A和B,分别在它的两个半平面α、β内作垂直于棱的线段AC、BD,已知AB=2a,AC=BD=a,求CD的长.
解析: 在α内作CH![]() AB,连结BH、HD,则BH
AB,连结BH、HD,则BH![]() AC,∴BH=a,BH⊥AB.而BD⊥AB,
AC,∴BH=a,BH⊥AB.而BD⊥AB,
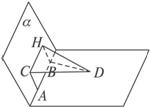
∴∠HBD为二面角αABβ的平面角,∠HBD=120°.
∴HD2=HB2+BD2-2HB·BDcos120°=3a2.
∵CH![]() AB,∴CH=2a,CH⊥平面HBD.
AB,∴CH=2a,CH⊥平面HBD.
∴CH⊥HD.
从而CD2=CH2+HD2=4a2+3a2=7a2.
∴CD=![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目