题目内容
【题目】某中学为了解高二学生对“地方历史”校本课程的喜欢是否与在本地成长有关,在全校高二学生中随机抽取了20名,得到一组不完全的统计数据如下表:
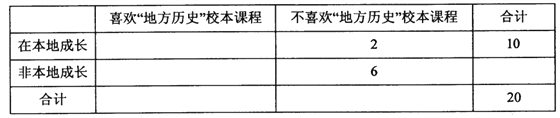
(1)补齐上表数据,并分别从被抽取的喜欢“地方历史”校本课程与不喜欢“地方历史”校本课程的学生中各选1名做进一步访谈,求至少有1名学生属于在本地成长的概率;
(2)试回答:能否在犯错误的概率不超过0.10的前提下认为“是否喜欢地方历史校本课程与在本地成长有关”.
附:

(参考公式: 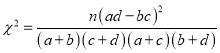 ,其中
,其中![]() )
)
【答案】(1) ![]() (2) 能在犯错误的概率不超过0.10的前提下认为“是否喜欢‘地方历史’校本课程与本地成长有关”
(2) 能在犯错误的概率不超过0.10的前提下认为“是否喜欢‘地方历史’校本课程与本地成长有关”
【解析】试题分析:(1)根据给出数据可以补齐表格,喜欢“地方历史”校本课程的12名学生中抽取1人,在本地成长的概率为![]() ;在不喜欢“地方历史”校本课程的8名学生中抽取1人,在本地成长的概率为
;在不喜欢“地方历史”校本课程的8名学生中抽取1人,在本地成长的概率为![]() ;设从中抽取的2名学生中至少有1名学生是在本地成长的事件为
;设从中抽取的2名学生中至少有1名学生是在本地成长的事件为![]() ,则
,则![]() 即得解;
即得解;
(2)![]()
![]()
![]() ,即可下结论.
,即可下结论.
试题解析:
(1)补齐表格如下:
喜欢“地方历史校本”课程 | 不喜欢“地方历史校本”课程 | 合计 | |
在本地成长 | 8 | 2 | 10 |
非本地成长 | 4 | 6 | 10 |
合计 | 12 | 8 | 20 |
由上表知,在喜欢“地方历史”校本课程的12名学生中抽取1人,在本地成长的概率为![]() ;在不喜欢“地方历史”校本课程的8名学生中抽取1人,在本地成长的概率为
;在不喜欢“地方历史”校本课程的8名学生中抽取1人,在本地成长的概率为![]() ;
;
设从中抽取的2名学生中至少有1名学生是在本地成长的事件为![]() ,则
,则
![]() .
.
(2)![]()
![]()
![]() ,
,
答:能在犯错误的概率不超过0.10的前提下认为“是否喜欢‘地方历史’校本课程与本地成长有关”.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目


