题目内容
(理)若数列 前8项的值各异,且
前8项的值各异,且 对任意的
对任意的 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍 前8项值的数列为( )
前8项值的数列为( )
A. | B.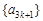 | C. | D. |
B
解析试题分析:因为,数列 前8项的值各异,且
前8项的值各异,且 对任意的
对任意的 都成立,所以,该数列为周期为8的周期数列。为使数列中可取遍
都成立,所以,该数列为周期为8的周期数列。为使数列中可取遍 前8项值,必须保证项数被8除的余数可以取到1,2,3,4,5,6,7,8。经验证A,B,D,都不可以,因为它们全部是奇数组成的,被8除的余数只能是奇数。故选B。
前8项值,必须保证项数被8除的余数可以取到1,2,3,4,5,6,7,8。经验证A,B,D,都不可以,因为它们全部是奇数组成的,被8除的余数只能是奇数。故选B。
考点:本题主要考查数列的概念及性质,数的整除性。
点评:简单题,关键是理解为使数列中可取遍 前8项值,必须保证项数被8除的余数可以取到1,2,3,4,5,6,7,8。
前8项值,必须保证项数被8除的余数可以取到1,2,3,4,5,6,7,8。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
数列 中的
中的 一个值等于
一个值等于
A. | B. | C. | D. |
在数列{ }中,若
}中,若 ,则
,则 ( )
( )
| A.1 | B.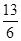 | C.2 | D.1.5 |
试探究下列一组数列的基本规律:0,2,6,14,30,…,根据规律写出第6个符合规律的数,这个数是( )
| A.60 | B.62 | C.64 | D.94 |
数列 的一个通项公式是( )
的一个通项公式是( )
A. | B. | C. | D. |
若数列{an}满足 -
- =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{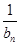 }为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
}为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
| A.10 | B.100 | C.200 | D.400 |
 是单位圆上一点,一个动点从点
是单位圆上一点,一个动点从点 出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周.
出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周. 秒时,动点到达点
秒时,动点到达点 ,
, 秒时动点到达点
秒时动点到达点 .设
.设 ,其纵坐标满足
,其纵坐标满足 .
.
 ;
; ,求
,求 的取值范围.
的取值范围. ,
, ,
, ,
, ,…为梯形数.根据图形的构成,记此数列的第
,…为梯形数.根据图形的构成,记此数列的第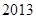 项为
项为 ,则
,则 ( )
( )




