题目内容
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数 ,
, ,
, ,
, ,…为梯形数.根据图形的构成,记此数列的第
,…为梯形数.根据图形的构成,记此数列的第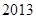 项为
项为 ,则
,则 ( )
( )
A. | B. | C. | D. |
D
解析试题分析:分析已知条件,寻求项与项之间的联系,是解题关键,由已知可得:
累加得: ,
, ,选D.
,选D.
考点:1、数列的概念;2、累加法.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
在数列1,1,2,3,5,8,x,21,34,55,…中, 等于( )
等于( )
| A.11 | B.12 | C.13 | D.14 |
两列数如下:7,10,13,16,19,22,25,28,31,......7,11,15,19,23,27,31,35,39,......第1个相同的数是7,第10个相同的数是( )
| A.115 | B.127 | C.139 | D.151 |
(理)若数列 前8项的值各异,且
前8项的值各异,且 对任意的
对任意的 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍 前8项值的数列为( )
前8项值的数列为( )
A. | B.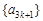 | C. | D. |
如图,第(1)个图案由1个点组成,第(2)个图案由3个点组成,第(3)个图案由7个点组成,第(4)个图案由13个点组成,第(5)个图案由21个点组成,……,依此类推,根据图案中点的排列规律,第100个图形由多少个点组成( )
| A.9900 | B.9901 | C.9902 | D.9903 |
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
| A.1011 | B.1012 | C.2013 | D.2014 |
数列{ }中,
}中, ,则
,则 为( )
为( )
| A.-3 | B.-11 | C.-5 | D.19 |
 ,b=
,b= ,且x∈
,且x∈ .
. ,求正实数λ的值.
,求正实数λ的值.