题目内容
【题目】将一张纸沿直线l对折一次后,点A(0,4)与点B(8,0)重叠,点C(6,8)与点D(m,n)重叠.
(1)求直线l的方程;
(2)求m+n的值;
(3)直线l上是否存在一点P,使得||PB|﹣|PC||存在最大值,如果存在,请求出最大值,以及此时点P的坐标;如果不存在,请说明理由.
【答案】
(1)解:设线段AB的中点为N,则点N(4,2),且 ![]()
则直线l的方程为2x﹣y﹣6=0
(2)解:设直线CD的方程为x+2y+C'=0
∵C(6,8)在直线CD上,∴C'=﹣22,则直线CD的方程为x+2y﹣22=0
设直线CD与直线l的交点为M, ![]()
![]()
则 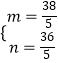 ,∴
,∴ ![]()
(3)解:假设直线l上存在点P,
∵||PB|﹣|PC||=||PA|﹣|PC||≥|AC|
当且仅当P,A,C三点共线时,等号成立
直线AC的方程为x﹣3y+12=0
∴ ![]() ,∴P(6,6)
,∴P(6,6)
【解析】(1)设线段AB的中点为N,则点N(4,2),且 ![]() ,即可求出直线l的方程;(2)求出直线CD的方程,可得直线CD与直线l的交点坐标,即可求m+n的值;(3)假设直线l上存在点P,利用||PB|﹣|PC||=||PA|﹣|PC||≥|AC|,得出结论.
,即可求出直线l的方程;(2)求出直线CD的方程,可得直线CD与直线l的交点坐标,即可求m+n的值;(3)假设直线l上存在点P,利用||PB|﹣|PC||=||PA|﹣|PC||≥|AC|,得出结论.

练习册系列答案
相关题目