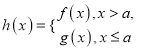题目内容
【题目】已知![]() 是偶函数,
是偶函数,![]() .
.
(1)求![]() 的值,并判断函数
的值,并判断函数![]() 在
在![]() 上的单调性,说明理由;
上的单调性,说明理由;
(2)设![]() ,若函数
,若函数![]() 与
与![]() 的图像有且仅有一个交点,求实数
的图像有且仅有一个交点,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的一个函数
上的一个函数![]() ,如果存在一个常数
,如果存在一个常数![]() ,使得式子
,使得式子![]() 对一切大于1的自然数
对一切大于1的自然数![]() 都成立,则称函数
都成立,则称函数![]() 为“
为“![]() 上的
上的![]() 函数”(其中,
函数”(其中,![]() ).试判断函数
).试判断函数![]() 是否为“
是否为“![]() 上的
上的![]() 函数”,若是,则求出
函数”,若是,则求出![]() 的最小值;若不是,则说明理由.(注:
的最小值;若不是,则说明理由.(注:![]() ).
).
【答案】(1)![]() ,递减;理由见解析;(2)
,递减;理由见解析;(2)![]() ;(3)是,
;(3)是,![]() .
.
【解析】
(1)由偶函数的定义可得f(﹣x)=f(x),结合对数函数的运算性质,解方程可得所求值;函数h(x)=f(x)![]() x=log4(4x+1)﹣x在R上递减,运用单调性的定义和对数函数的单调性,即可证明;
x=log4(4x+1)﹣x在R上递减,运用单调性的定义和对数函数的单调性,即可证明;
(2)由题意可得log4(4x+1)![]() x=log4(a2x
x=log4(a2x![]() a)有且只有一个实根,可化为2x+2﹣x=a2x
a)有且只有一个实根,可化为2x+2﹣x=a2x![]() a,即有a
a,即有a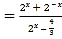 ,化为a﹣1
,化为a﹣1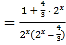 ,运用换元法和对勾函数的单调性,即可得到所求范围.
,运用换元法和对勾函数的单调性,即可得到所求范围.
(3)利用![]() 求解即可
求解即可
(1)f(x)=log4(4x+1)+kx是偶函数,
可得f(﹣x)=f(x),即log4(4﹣x+1)﹣kx=log4(4x+1)+kx,
即有log4![]() 2kx,可得log44﹣x=﹣x=2kx,
2kx,可得log44﹣x=﹣x=2kx,
由x∈R,可得k![]() ;
;
又函数h(x)=f(x)![]() x=log4(4 x+1)﹣x=
x=log4(4 x+1)﹣x=![]() 在R上递减,
在R上递减,
理由:设x1<x2,则h(x1)﹣h(x2)=log4(![]() )﹣log4(
)﹣log4(![]() )
)
=log4(4﹣x1+1)﹣log4(4﹣x2+1),
由x1<x2,可得﹣x1>﹣x2,可得log4(4﹣x1+1)>log4(4﹣x2+1),
则h(x1)>![]() x在R上递减;
x在R上递减;
(2)g(x)=log4(a2x![]() a),若函数f(x)与g(x)的图象有且仅有一个交点,
a),若函数f(x)与g(x)的图象有且仅有一个交点,
即为log4(4x+1)![]() x=log4(a2x
x=log4(a2x![]() a)有且只有一个实根,
a)有且只有一个实根,
可化为2x+2﹣x=a2x![]() a,
a,
即有a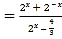 ,化为a﹣1
,化为a﹣1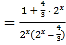 ,
,
可令t=1![]() 2x(t>1),则2x
2x(t>1),则2x![]() ,
,
则a﹣1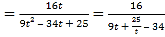 ,
,
由9t![]() 34在(1,
34在(1,![]() )递减,(
)递减,(![]() ,+∞)递增,
,+∞)递增,
可得9t![]() 34的最小值为2
34的最小值为2![]() 34=﹣4,
34=﹣4,
当a﹣1=﹣4时,即a=﹣3满足两图象只有一个交点;
当t=1时,9t![]() 34=0,可得a﹣1>0时,即a>1时,两图象只有一个交点,
34=0,可得a﹣1>0时,即a>1时,两图象只有一个交点,
综上可得a的范围是(1,+∞)∪{﹣3}.
(3)![]() 是
是![]() 函数,理由如下:由题当任意的
函数,理由如下:由题当任意的![]() ,有
,有![]()
因为![]() 单调递增,则
单调递增,则![]() ,故
,故![]() 的最小值为
的最小值为![]()