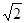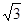题目内容
如图,直三棱柱ABC-A1B1C1中,AC=BC=1,∠ACB=90°,AA1=
,D是A1B1中点.
(1)求证C1D⊥平面AA1B1B;
(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF?并证明你的结论.

| 2 |
(1)求证C1D⊥平面AA1B1B;
(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF?并证明你的结论.

(1)证明:∵ABC-A1B1C1是直三棱柱,
∴A1C1=B1C1=1,且∠A1C1B1=90°.
又D是A1B1的中点,∴C1D⊥A1B1.
∵AA1⊥平面A1B1C1,C1D?平面A1B1C1,
∴AA1⊥C1D,∴C1D⊥平面AA1B1B.
(2)作DE⊥AB1交AB1于E,延长DE交BB1于F,连接C1F,则AB1⊥平面C1DF,点F即为所求.
事实上,∵C1D⊥平面AA1B1B,AB1?平面AA1B1B,
∴C1D⊥AB1.又AB1⊥DF,DF∩C1D=D,
∴AB1⊥平面C1DF.
四边形AA1B1B为正方形,此时点F为B1B的中点.
∴A1C1=B1C1=1,且∠A1C1B1=90°.
又D是A1B1的中点,∴C1D⊥A1B1.
∵AA1⊥平面A1B1C1,C1D?平面A1B1C1,
∴AA1⊥C1D,∴C1D⊥平面AA1B1B.
(2)作DE⊥AB1交AB1于E,延长DE交BB1于F,连接C1F,则AB1⊥平面C1DF,点F即为所求.
事实上,∵C1D⊥平面AA1B1B,AB1?平面AA1B1B,
∴C1D⊥AB1.又AB1⊥DF,DF∩C1D=D,
∴AB1⊥平面C1DF.
四边形AA1B1B为正方形,此时点F为B1B的中点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
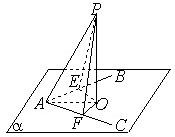
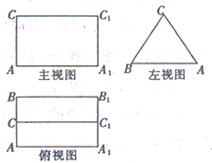
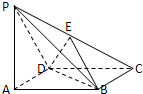
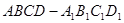 中,
中,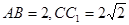 ,
, 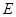 为
为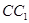 的中点,则点
的中点,则点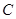 到平面
到平面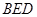 的距离为()
的距离为()