题目内容
以下是某地搜集到的新房屋的销售价格 和房屋的面积
和房屋的面积 的数据:
的数据:
房屋面积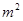 | 110 | 90 | 80 | 100 | 120 |
| 销售价格(万元) | 33 | 31 | 28 | 34 | 39 |
(2)求线性回归方程;
(3)据(2)的结果估计当房屋面积为
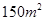 时的销售价格.
时的销售价格.(提示:
 ,
, 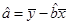 ,
,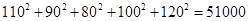 ,
,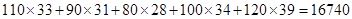 )
)
(1)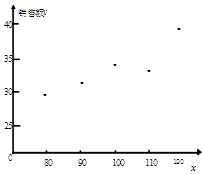
(2)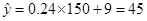
(3)当 时,销售价格的估计值为:
时,销售价格的估计值为: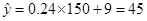 (万元)
(万元)
解析试题分析:解:(1)数据对应的散点图如图所示: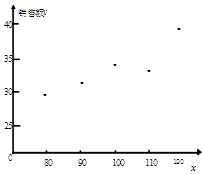 2分
2分
(2) 3分
3分 4分
4分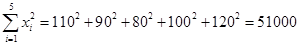 , 5分
, 5分 6分
6分
∴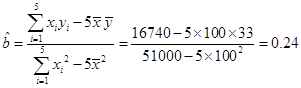 , 8分
, 8分 10分
10分
∴回归直线方程为.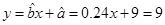 12分
12分
(3)据(2),当 时,销售价格的估计值为:
时,销售价格的估计值为: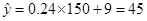 (万元) 14分
(万元) 14分
考点:线性回归方程的求解和运用
点评:解决试题的关键是利用散点图分析回归模型,然后借助于公式得到结论,属于基础题。

练习册系列答案
相关题目
延迟退休年龄的问题,近期引发社会的关注.人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
| 月收入(元) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) | [6000,7000) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 反对人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(2)若对月收入在[1000,2000),[4000,5000)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下图:若加工时间 与零件个数
与零件个数 之间有较好的线性相关关系。(
之间有较好的线性相关关系。(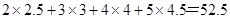 )
)
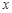 | 2 | 3 | 4 | 5 |
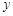 | 2.5 | 3 | 4 | 4.5 |
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间。
(附:回归方程系数公式
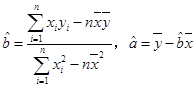 )
) (本题10分) 为了解高二学年女生身高情况,对高二(10)班女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 | 频数 | 频率 |
| 145.5~149.5 | 1 | 0.02 |
| 149.5~153.5 | 4 | 0.08 |
| 153.5~157.5 | 20 | 0.40 |
| 157.5~161.5 | 15 | 0.30 |
| 161.5~165.5 | 8 | 0.16 |
| 165.5~169.5 | m | n |
| 合 计 | M | N |
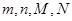 所表示的数分别是多少?
所表示的数分别是多少?(2)若该校高二学年共有女生500人,试估计高二女生中身高在161.5以上的人数。
(本小题12分)本某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
| 锻炼时间(分钟) | 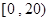 |  |  |  | 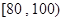 |  |
| 人数 | 40 | 60 | 80 | 100 | 80 | 40 |
课外体育锻炼时间的平均值(同一组中的数据用该区间的组中值作代表);
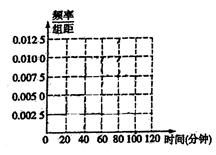
(2)现采用分层抽样的方法抽取容量为20的样本,
①应抽取多少名课外体育锻炼时间为
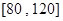 分钟的学生;
分钟的学生;②若从①中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均为
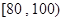 分钟的概率。
分钟的概率。 
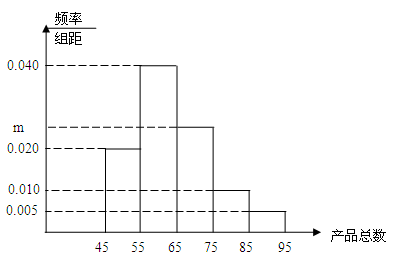
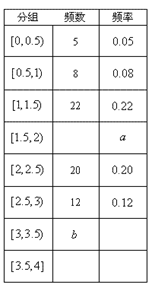
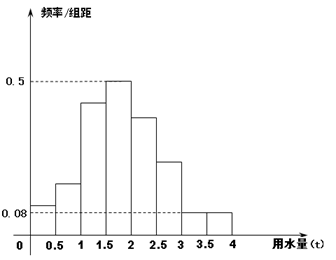
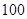 户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).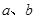 的值,并估计该社区家庭月均用水量不超过
的值,并估计该社区家庭月均用水量不超过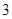 吨的频率;
吨的频率; 、
、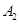 、
、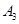 是户月均用水量为
是户月均用水量为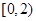 的居民代表,
的居民代表, 、
、 是户月均用水量为
是户月均用水量为 的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表
的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表