Question

【题目】当实数x，y满足 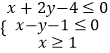时，1≤ax+y≤4恒成立，则实数a的取值范围是 ．

Answer 1

【答案】
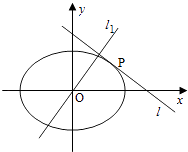
【解析】解：由约束条件作可行域如图，
联立 ，解得C（1， ）．
联立 ，解得B（2，1）．
在x﹣y﹣1=0中取y=0得A（1，0）．
要使1≤ax+y≤4恒成立，
则 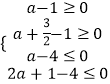，解得：1 ．
∴实数a的取值范围是 ．
解法二：令z=ax+y，
当a＞0时，y=﹣ax+z，在B点取得最大值，A点取得最小值，
可得 ，即1≤a≤ ；
当a＜0时，y=﹣ax+z，在C点取得最大值，
①a＜﹣1时，在B点取得最小值，可得 ，解得0≤a≤ （不符合条件，舍去）
②﹣1＜a＜0时，在A点取得最小值，可得 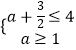，解得1≤a≤ （不符合条件，舍去）
综上所述即：1≤a≤ ；
故答案为： ．

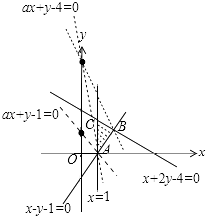
由约束条件作出可行域，再由1≤ax+y≤4恒成立，结合可行域内特殊点A，B，C的坐标满足不等式列不等式组，求解不等式组得实数a的取值范围．