题目内容
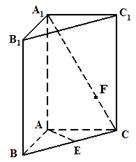
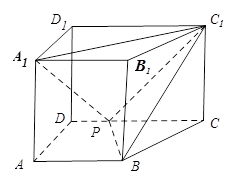
如图,直三棱柱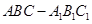 的底面
的底面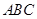 是等腰直角三角形,
是等腰直角三角形,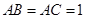 ,侧棱
,侧棱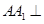 底面
底面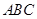 ,且
,且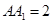 ,
,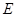 是
是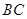 的中点,
的中点,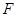 是
是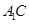 上的点.
上的点.
(1)求异面直线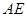 与
与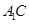 所成角
所成角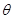 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
(2)若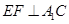 ,求线段
,求线段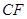 的长.
的长.
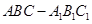 的底面
的底面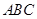 是等腰直角三角形,
是等腰直角三角形,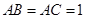 ,侧棱
,侧棱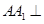 底面
底面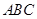 ,且
,且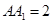 ,
,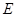 是
是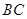 的中点,
的中点,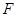 是
是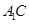 上的点.
上的点.(1)求异面直线
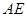 与
与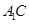 所成角
所成角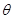 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);(2)若
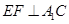 ,求线段
,求线段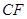 的长.
的长.
(1)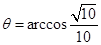 ,(2)
,(2)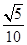 .
.
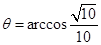 ,(2)
,(2)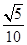 .
.试题分析:(1)求异面直线所成角,关键在于利用平行,将所求角转化为某一三角形中的内角.因为条件有中点,所以从中位线上找平行. 取
 的中点
的中点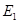 ,连
,连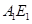 ,则
,则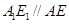 ,即
,即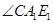 即为异面直线
即为异面直线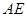 与
与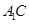 所成的角
所成的角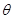 .分别求出三角形三边,再利用余弦定理求角.
.分别求出三角形三边,再利用余弦定理求角. 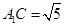 ,
, ,
,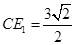 ,
,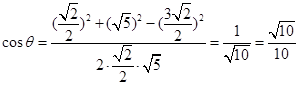 ,
,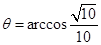 ,(2)求线段长,可利用空间向量坐标进行计算. 设
,(2)求线段长,可利用空间向量坐标进行计算. 设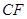 的长为
的长为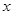 ,
,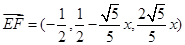 ,
,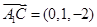 ,由
,由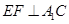 知
知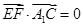 可得
可得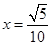 ,∴线段
,∴线段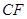 的长为
的长为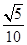
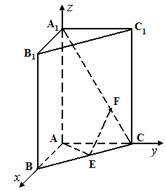
解:(1)取
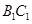 的中点
的中点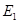 ,连
,连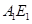 ,则
,则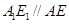 ,即
,即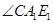 即为异面直线
即为异面直线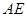 与
与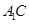 所成的角
所成的角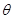 . (2分)
. (2分)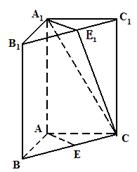 连
连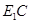 .
.在
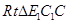 中,由
中,由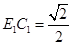 ,
,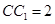
知
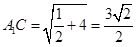
在
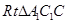 中,由
中,由 ,
,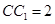 知
知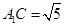 (4分)
(4分)在
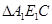 中,
中,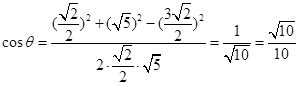
 ∴
∴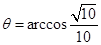 (6分)
(6分)(2)以
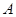 为原点,建立如图空间直角坐标系,设
为原点,建立如图空间直角坐标系,设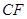 的长为
的长为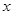
则各点的坐标为,
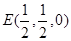 ,
,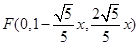 ,
,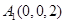 ,
,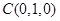 (2分)
(2分)∴
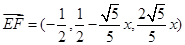 ,
,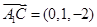
由
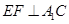 知
知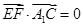 (4分)
(4分)即
 ,解得
,解得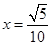
∴线段
 的长为
的长为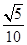 (6分)
(6分)
练习册系列答案
相关题目
 的边长为2,
的边长为2,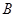 ,
,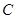 分别为
分别为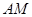 ,
,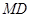 的中点,在五棱锥
的中点,在五棱锥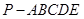 中,
中,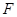 为棱
为棱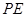 的中点,平面
的中点,平面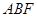 与棱
与棱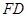 ,
,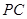 分别交于
分别交于 ,
,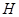 .
.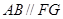 ;
;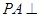 底面
底面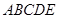 ,且
,且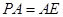 ,求直线
,求直线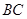 与平面
与平面 的长.
的长.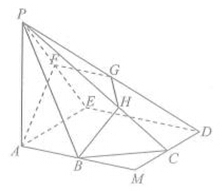
 的正方形
的正方形 中,点
中,点 在线段
在线段 上,且
上,且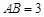 ,
,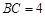 ,作
,作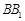 //
//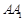 ,分别交
,分别交 ,
,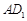 于点
于点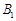 ,
,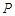 ,作
,作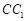 //
//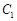 ,
,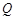 ,将该正方形沿
,将该正方形沿 与
与 .
.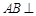 平面
平面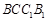 ;
; 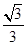 ,求|BE|的最小值.
,求|BE|的最小值.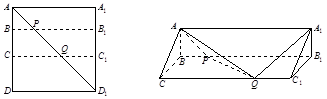
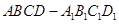 底面
底面 直角梯形,
直角梯形,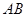 ∥
∥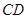 ,
,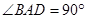 ,
,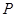 是棱
是棱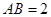 ,
,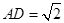 ,
,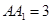 ,
,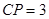 ,
,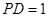 .
.
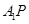 与
与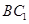 所成的角;
所成的角;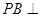 平面
平面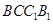 .
.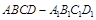 中,底面
中,底面 是矩形,
是矩形,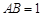 ,
,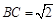 ,
,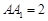 ,
,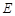 是侧棱
是侧棱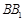 的中点.
的中点.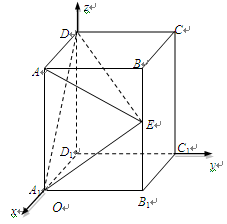
 平面
平面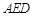 ;
;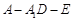 的大小.
的大小.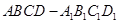 中,底面
中,底面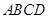 和侧面
和侧面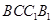 都
都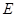 是
是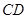 的中点,
的中点,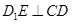 ,
,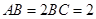 .
.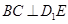
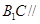 平面
平面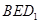 ;
;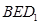 所成的锐二面角的大小为
所成的锐二面角的大小为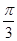 ,求线段
,求线段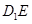 的长度.
的长度.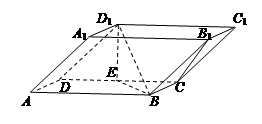

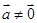 ,
,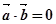 ,则
,则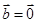 ; ②若
; ②若 ,则
,则 ;
;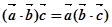 ; ④
; ④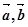 为非零不共线,若
为非零不共线,若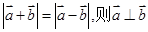 ;
;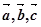 非零不共线,则
非零不共线,则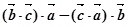 与
与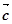 垂直
垂直