题目内容
19.求下列函数的定义域和值域:(1)y=tan(x+$\frac{π}{4}$);
(2)y=$\sqrt{\sqrt{3}-tanx}$.
分析 根据正切函数的定义域和值域的性质进行求解即可.
解答 解:(1)y=tan(x+$\frac{π}{4}$);
由x+$\frac{π}{4}$≠kπ+$\frac{π}{2}$,得x≠kπ+$\frac{π}{4}$,即函数的定义域为{x|x≠kπ+$\frac{π}{4}$,k∈Z}.函数的值域为(-∞,+∞).
(2)y=$\sqrt{\sqrt{3}-tanx}$.
由$\sqrt{3}$-tanx≥0得tanx≤$\sqrt{3}$,即kπ-$\frac{π}{2}$<x≤kπ+$\frac{π}{3}$,即函数的定义域为(kπ-$\frac{π}{2}$,kπ+$\frac{π}{3}$],k∈Z,
∵$\sqrt{3}$-tanx≥0,∴y≥0,即函数的值域为[0,+∞).
点评 本题主要考查正切函数的定义域和值域求解,要求熟练掌握正切函数的图象和性质.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
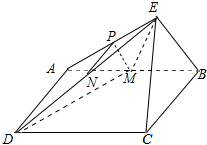 如图,已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.求证:MN⊥EA.
如图,已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.求证:MN⊥EA.