题目内容
11．
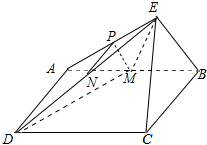如图，已知四边形ABCD为平行四边形，BC⊥平面ABE，AE⊥BE，M为线段AB的中点，N为线段DE的中点，P为线段AE的中点．求证：MN⊥EA．
分析 证明MP⊥AE，NP⊥AE，可得AE⊥平面MNP，从而可证明MN⊥EA．
解答 证明：∵AE⊥BE，MP∥BE，∴MP⊥AE，
又BC⊥平面ABE，AE?平面ABE，∴BC⊥AE，
∵N为DE的中点，P为AE的中点，∴NP∥AD，
∵AD∥BC，∴NP∥BC，
∴NP⊥AE，
又∵NP∩MP=P，NP，MP?平面PMN，
∴AE⊥平面MNP，
∵MN?平面MNP，
∴MN⊥EA．
点评 本题考查线面垂直的判定与性质，考查学生分析解决问题的能力，正确运用线面垂直的判定与性质是关键．
练习册系列答案
相关题目
1．设直线x-3y+m=0（m≠0）与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）两条渐近线分别交于点A、B，若点P（m，0）满足（$\overrightarrow{PA}$+$\overrightarrow{PB}$）⊥$\overrightarrow{AB}$，则该双曲线的离心率是（ ）
| A． | $\frac{\sqrt{5}}{4}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\frac{5}{2}$ | D． | $\sqrt{5}$ |