题目内容
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
(1)分布列详见解析,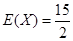 ;(2)
;(2)
解析试题分析:(1)乙的得分分为4类:①所选的3道题都打错,得分为-15,概率为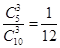 ;②所选的3道题有2道答错1道答对,得分为0,概率为
;②所选的3道题有2道答错1道答对,得分为0,概率为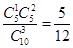 ;③所选的3道题1道答错2道答对,得分为15,概率为
;③所选的3道题1道答错2道答对,得分为15,概率为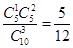 ;④所选的3道题全答对,得分为30分,概率为
;④所选的3道题全答对,得分为30分,概率为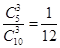 ,从而写出分布列,并求期望;(2) 甲、乙入选的事件分别为
,从而写出分布列,并求期望;(2) 甲、乙入选的事件分别为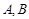 ,则甲、乙至少答对两道题,分别求其概率,所求事件的概率为
,则甲、乙至少答对两道题,分别求其概率,所求事件的概率为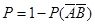 .
.
(1)设乙答题所得分数为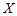 ,则
,则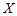 的可能取值为
的可能取值为 . 1分
. 1分
且
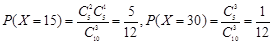 5分
5分
乙的得分的分布列如右表,且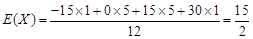 8分
8分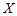
-15 0 15 30 
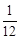
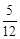
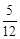
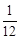
(2)由已知甲、乙至少答对2题才能入选, 记甲、乙入选的
事件分别为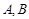 ,则由(1)知,
,则由(1)知,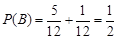 ,
,
又甲回答3题可以视为独立重复试验,故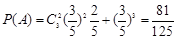 ,
,
于是甲、乙至少有一人入选的概率 12分
12分
考点:1、离散型随机变量的分布列和期望;2、对立事件的概率.

练习册系列答案
相关题目
 名同学.
名同学.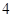 人参加班级
人参加班级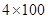 接力比赛,则同学丙不跑第一棒的安排方法有多少种?
接力比赛,则同学丙不跑第一棒的安排方法有多少种?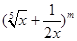 的展开式中第2项为常数项
的展开式中第2项为常数项 ,其中
,其中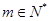 ,且展开式按
,且展开式按 的降幂排列.
的降幂排列. 及
及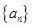 中,
中, ,
,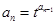 ,
,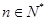 ,求证:
,求证: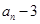 能被4整除.
能被4整除.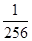 相等,求x的值.
相等,求x的值.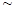 75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.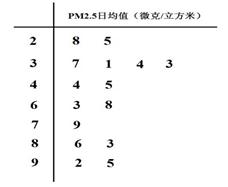
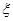 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求 展开式中各项系数和为3,则
展开式中各项系数和为3,则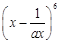 的展开式中的常数项为________
的展开式中的常数项为________