题目内容
已知二项式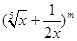 的展开式中第2项为常数项
的展开式中第2项为常数项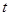 ,其中
,其中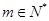 ,且展开式按
,且展开式按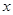 的降幂排列.
的降幂排列.
(1)求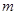 及
及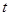 的值.
的值.
(2)数列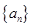 中,
中,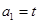 ,
,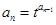 ,
,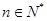 ,求证:
,求证: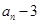 能被4整除.
能被4整除.
(1)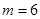 ,
,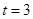 ;(2))证明过程详见解析.
;(2))证明过程详见解析.
解析试题分析:(1)由展开式中第2项为常数项,则可根据二项式展开式的第2项展开式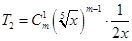 中未知数
中未知数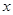 的指数为0,从而求出
的指数为0,从而求出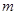 的值,将
的值,将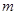 的值代回第2项展式可求出
的值代回第2项展式可求出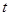 的值;(2)可利用数学归纳法来证明,①当
的值;(2)可利用数学归纳法来证明,①当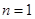 时,
时,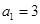 ,
,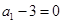 ,能被4整除,显然命题成立;②假设当n=k时,
,能被4整除,显然命题成立;②假设当n=k时, 能被4整除,即
能被4整除,即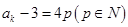 .那么当n =k+1时,
.那么当n =k+1时,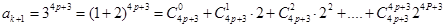
=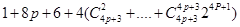 =
=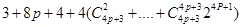
=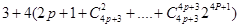 显然
显然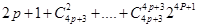 是非负整数,
是非负整数,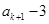 能被4整除.
能被4整除.
由①、②可知,命题对一切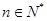 都成立.
都成立.
试题解析:(1) 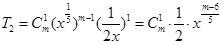 , 2分
, 2分
故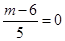 ,
,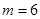 ,
,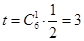 . 4分
. 4分
(2)证明:①当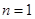 时,
时,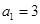 ,
,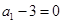 ,能被4整除.
,能被4整除.
②假设当n=k时, 能被4整除,即
能被4整除,即 ,其中p是非负整数.
,其中p是非负整数.
那么当n =k+1时,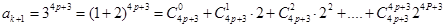
=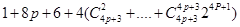 =
=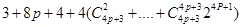
=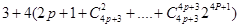 显然
显然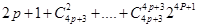 是非负整数,
是非负整数,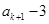 能被4整除.
能被4整除.
由①、②可知,命题对一切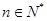 都成立. 10分
都成立. 10分
考点:1.二项式定理;2.数学归纳法.

练习册系列答案
相关题目
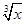 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-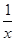 )2n的展开式中:
)2n的展开式中: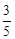 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.