题目内容
17．已知函数f（x）是定义在R上周期为3的周期函数，当x∈[0，3）时，$f（x）=|{x^2}-2x+\frac{1}{2}|$，则函数f（x）在[-3，4]上的零点的个数为（ ）| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
分析 由条件画出函数f（x）的图象，数形结合可得函数f（x）在[-3，4]上的零点的个数．
解答 
解：根据函数f（x）是定义在R上周期为3的周期函数，当x∈[0，3）时，$f（x）=|{x^2}-2x+\frac{1}{2}|$，
画出函数f（x）的图象，如图所示：
数形结合可得函数f（x）在[-3，4]上的零点的个数为5，
故选：D．
点评 本题主要考查方程的根的存在性及个数判断，体现了化归与转化、数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
7．多面体MN-ABCD的底面ABCD矩形，其正（主）视图和侧（左）视图如图，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则该多面体的体积为（ ）
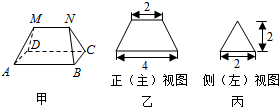
| A． | $\frac{16}{3}$ | B． | $\sqrt{6}$ | C． | $\frac{20}{3}$ | D． | 6 |
8．
函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则此函数的解析式为（ ）
函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则此函数的解析式为（ ）| A． | y=3sin（$\frac{π}{4}$x+$\frac{π}{4}$） | B． | y=3sin（$\frac{π}{4}$x+$\frac{3π}{4}$） | C． | y=3sin（$\frac{π}{2}$x+$\frac{π}{4}$） | D． | y=3sin（$\frac{π}{2}$x+$\frac{3π}{4}$） |
如图（1）所示，以线段BD为直径的圆经过A，C两点，且AB=BC=1，BD=2，延长DA，CB交于点P，将△PAB沿AB折起，使点P至点P′位置得到如图（2）所示的空间图形，其中点P′在平面ABCD内的射影恰为线段AD的中点Q．
如图，射线OA，OB所在的直线的方向向量分别为$\overrightarrow{d_1}=（{1，k}）$，$\overrightarrow{d_2}=（{1，-k}）（{k＞0}）$，点P在∠AOB内，PM⊥OA于M，PN⊥OB于N；
6．某几何体的三视图（单位：cm）如图，则这个几何体的体积为（ ）cm3．
| A． | $\sqrt{3}$ | B． | $2\sqrt{3}$ | C． | $4\sqrt{3}$ | D． | $6\sqrt{3}$ |
如图，在直三角形ABC-A1B1C1中，M为AB1的中点，△CMB1为等边三角形