题目内容
12.已知点A(1-m,0),B(1+m,0),若圆C:x2+y2-8x-8y+31=0上存在一点P,使得$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,则m的最大值为6.分析 将圆的方程变成标准方程:(x-4)2+(y-4)2=1,从而可设P(4+cosθ,4+sinθ),根据已知条件知道△PAB为直角三角形,并且可求得AB中点为(1,0),从而得到P到该点的距离为|m|,根据两点间距离公式从而得到(3+cosθ)2+(4+sinθ)2=m2,将该式可变成26+10sin(θ+φ)=m2,这样即可求得m的最大值.
解答 解:圆C的方程变成:(x-4)2+(y-4)2=1;
∴设P(4+cosθ,4+sinθ),如图: 线段AB的中点坐标为(1,0),|AB|=2|m|;
线段AB的中点坐标为(1,0),|AB|=2|m|;
∴P点到线段AB中点的距离为|m|;
∴(3+cosθ)2+(4+sinθ)2=m2;
∴26+6cosθ+8sinθ=m2;
∴26+10sin(θ+φ)=m2,其中tanφ=$\frac{3}{4}$;
∴m2最大为36;
∴m的最大值为6.
故答案为:6.
点评 考查圆的标准方程,直角三角形的直角顶点到斜边的距离等于斜边的一半,中点坐标公式,两非零向量垂直的充要条件,以及利用三角函数设圆上点的坐标,两点间距离公式.

练习册系列答案
相关题目
2.已知命题ρ:将函数y=sin2x的图象向右平移$\frac{π}{6}$个单位后,对应函数的解析式为y=sin(2x-$\frac{π}{3}$);命题q:正切函数y=tanx在定义域内为增函数,则下列命题中为真命题的是( )
| A. | (¬ρ)∧(¬q) | B. | (¬ρ)∧q | C. | ρ∧(¬q) | D. | ρ∧q |
7.多面体MN-ABCD的底面ABCD矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为( )
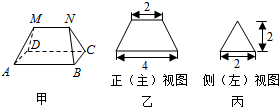

| A. | $\frac{16}{3}$ | B. | $\sqrt{6}$ | C. | $\frac{20}{3}$ | D. | 6 |

 如图,在平行四边形ABCD中,AB=4,点E为边DC的中点,AE与BC的延长线交于点F,且AE平分∠BAD,作DG⊥AE,垂足为G,若DG=1,则AF的长为4$\sqrt{3}$.
如图,在平行四边形ABCD中,AB=4,点E为边DC的中点,AE与BC的延长线交于点F,且AE平分∠BAD,作DG⊥AE,垂足为G,若DG=1,则AF的长为4$\sqrt{3}$. 如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图(2)所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q.
如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图(2)所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q.