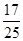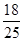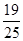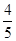题目内容
已知椭圆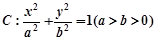 的焦点为
的焦点为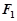
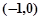 ,
,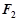
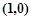 ,且经过点
,且经过点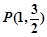 .
.
(Ⅰ)求椭圆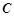 的方程;
的方程;
(Ⅱ)设过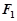 的直线
的直线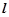 与椭圆
与椭圆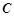 交于
交于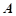 、
、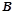 两点,问在椭圆
两点,问在椭圆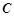 上是否存在一点
上是否存在一点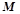 ,使四边形
,使四边形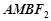 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线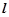 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
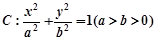 的焦点为
的焦点为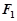
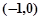 ,
,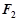
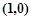 ,且经过点
,且经过点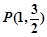 .
.(Ⅰ)求椭圆
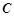 的方程;
的方程;(Ⅱ)设过
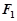 的直线
的直线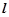 与椭圆
与椭圆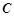 交于
交于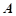 、
、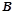 两点,问在椭圆
两点,问在椭圆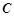 上是否存在一点
上是否存在一点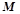 ,使四边形
,使四边形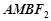 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线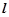 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.(Ⅰ)椭圆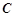 的方程为
的方程为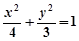 ;(Ⅱ)存在符合条件的直线
;(Ⅱ)存在符合条件的直线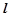 的方程为:
的方程为: .
.
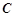 的方程为
的方程为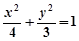 ;(Ⅱ)存在符合条件的直线
;(Ⅱ)存在符合条件的直线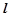 的方程为:
的方程为: .
.试题分析:(Ⅰ)已知椭圆
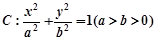 的焦点为
的焦点为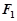
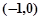 ,
,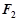
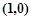 ,且经过点
,且经过点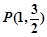 ,求椭圆
,求椭圆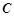 的方程,显然
的方程,显然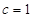 ,而
,而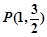 正好是过焦点,且垂直于
正好是过焦点,且垂直于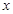 轴的弦的端点,故
轴的弦的端点,故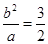 ,再由
,再由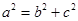 ,解出
,解出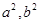 即可;(Ⅱ)设过
即可;(Ⅱ)设过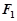 的直线
的直线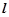 与椭圆
与椭圆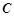 交于
交于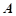 、
、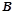 两点,问在椭圆
两点,问在椭圆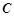 上是否存在一点
上是否存在一点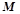 ,使四边形
,使四边形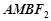 为平行四边形,若存在,求出直线
为平行四边形,若存在,求出直线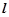 的方程,若不存在,请说明理由,此题是探索性命题,一般都是假设存在符合条件的点
的方程,若不存在,请说明理由,此题是探索性命题,一般都是假设存在符合条件的点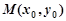 ,根据题意,若能求出直线
,根据题意,若能求出直线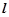 的方程,就存在,若不能求出直线
的方程,就存在,若不能求出直线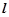 的方程,就不存在,此题设直线
的方程,就不存在,此题设直线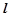 的方程为
的方程为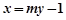 ,代入方程得
,代入方程得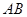 的中点为
的中点为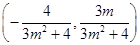 , 由于四边形
, 由于四边形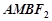 为平行四边形,
为平行四边形,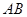 与
与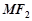 的中点重合,得
的中点重合,得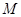 点坐标,代入椭圆方程求出
点坐标,代入椭圆方程求出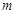 的值,从而得存在符合条件的直线
的值,从而得存在符合条件的直线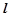 的方程为:
的方程为: .
.试题解析:(Ⅰ)
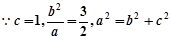 3分
3分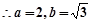 , 5分
, 5分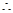 椭圆
椭圆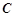 的方程为
的方程为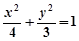 7分
7分(Ⅱ)假设存在符合条件的点
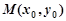 ,
,设直线
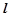 的方程为
的方程为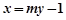 8分
8分由
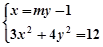 得:
得: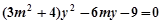 ,
,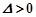 ,
,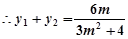 ,
,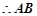 的中点为
的中点为 10分
10分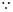 四边形
四边形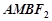 为平行四边形,
为平行四边形,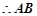 与
与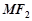 的中点重合,即:
的中点重合,即: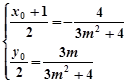
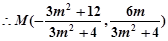 13分
13分把点
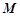 坐标代入椭圆
坐标代入椭圆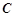 的方程得:
的方程得: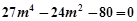
解得
 14分
14分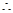 存在符合条件的直线
存在符合条件的直线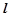 的方程为:
的方程为: 15分
15分
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
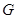 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆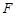 的直线
的直线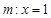 与椭圆
与椭圆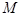 (点
(点 为椭圆
为椭圆 的直线
的直线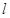 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线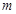 对称,并说明理由.
对称,并说明理由. 的焦点重合.
的焦点重合. 交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得
交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得 始终平分
始终平分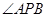 ?若存在,求出
?若存在,求出 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.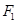 、
、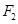 分别是椭圆
分别是椭圆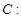
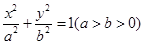 的左、右焦点,右焦点
的左、右焦点,右焦点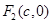 到上顶点的距离为2,若
到上顶点的距离为2,若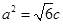
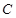 的方程;
的方程;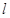 与椭圆
与椭圆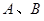 两点,若弦
两点,若弦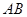 的中点为
的中点为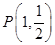 ,求直线
,求直线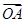 ·
·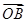 的值;
的值; ,若焦点在
,若焦点在 轴上的椭圆
轴上的椭圆 过点
过点 ,且其长轴长等于圆
,且其长轴长等于圆 的直径.
的直径. 作两条互相垂直的直线
作两条互相垂直的直线 与
与 ,
, 、
、 两点,
两点, ,设直线
,设直线 ,求弦
,求弦 长;
长; 面积的最大值.
面积的最大值.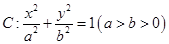 ,
,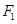 、
、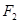 是其左右焦点,离心率为
是其左右焦点,离心率为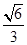 ,且经过点
,且经过点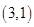 .
.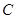 的标准方程;
的标准方程; 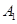 、
、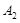 分别是椭圆长轴的左右端点,
分别是椭圆长轴的左右端点,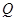 为椭圆上动点,设直线
为椭圆上动点,设直线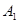
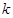 ,且
,且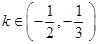 ,求直线
,求直线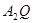 斜率的取值范围;
斜率的取值范围;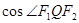 的最小值.
的最小值.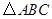 中,
中,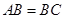 ,
, .若以
.若以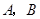 为焦点的椭圆经过点
为焦点的椭圆经过点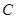 ,则该椭圆的离心率
,则该椭圆的离心率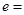 ( )
( )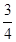

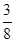
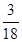
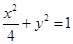 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于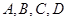 四点,则四边形
四点,则四边形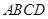 面积的最大值与最小值之差为( )
面积的最大值与最小值之差为( )