题目内容
【题目】已知函数
的定义域为
，当
时，
，且对任意的实数
，
，
恒成立，若数列
满足
（
）且
，则下列结论成立的是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
取x＝y＝0，可得f（0）f（0）＝f（0），分析可得f（0）＝1．取y＝﹣x＜0，f（x）f（﹣x）＝1，可得f（x）
1，设x1＜x2，则f（x1﹣x2）＝f（x1）f（﹣x2）
1，可得函数f（x）在R上单调递减．根据数列{an}满足f（an+1）f（
）＝1＝f（0）．可得an+1
0，a1＝f（0）＝1，可得：an+3＝an．进而得出结论．
对任意的实数x，y∈R，f（x）f（y）＝f（x+y）恒成立，
取x＝y＝0，则f（0）f（0）＝f（0），解得f（0）＝0或f（0）＝1．
当f（0）＝0时，
，得
余题意不符，故舍去.
所以f（0）＝1．
取y＝﹣x＜0，则f（x）f（﹣x）＝1，∴f（x）
，
设x1＜x2，则f（x1﹣x2）＝f（x1）f（﹣x2）1，∴f（x1）＞f（x2）．
∴函数f（x）在R上单调递减．
∵数列{
}满足f（an+1）f（）＝1＝f（0）．
∴
0，∵a1＝f（0）＝1，
∴
，
＝﹣2，
＝1，
，……．
∴
＝．
∴
＝，
＝
＝1．
＝，
＝＝﹣2．
∴f（）
1，f（）＝f（1）＜1．
∴f（）＞f（）．
而f（）＝f（），f（）＜1＜f（），
f（）＝f（
）＜f（）＝f（﹣2），
因此只有：C正确．
故选：C．
华东师大版一课一练系列答案
【题目】根据消费者心理学的研究，商品的销售件数与购买人数存在一定的关系，商家可以根据此调整相应的商品小手策略，以谋求商品更多销量，从而获取更多利润.某商场对购买人数和销售件数进行了统计对比，得到如下表格：
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
（参考公式：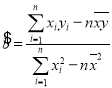
，
）
（1）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图：
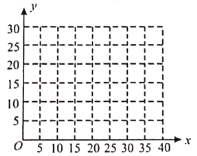
（2）根据（1）中所绘制的散点图，可得出购买人数与商品销售件数存在怎样的关系？并求出回归直线方程；（结果保留到小数点后两位）
（3）预测当进店人数为80人时，商品销售的件数.（结果保留整数）
【题目】已知数列
按如下规律分布（其中
表示行数，
表示列数），若
，则下列结果正确的是（ ）
第1列 | 第2列 | 第3列 | 第4列 | … | ||
第1行 | 1 | 3 | 9 | 19 | 33 | |
第2行 | 7 | 5 | 11 | 21 | ||
第3行 | 17 | 15 | 13 | 23 | ||
第4行 | 31 | 29 | 27 | 25 | ||
┇ |
A.
，
B.
，
C.
，
D.
，
