题目内容
已知椭圆的中心为O,长轴、短轴的长分别为2a,2b(a>b>0),A,B分别为椭圆上的两点,且OA⊥OB,过O点作OM⊥AB交AB于点M,求点M的轨迹。
点M的轨迹是以O为圆心, 为半径的圆。
为半径的圆。
 为半径的圆。
为半径的圆。以O点为坐标原点,长轴所在直线为x轴,短轴所在直线为y轴建立平面直角坐标系,则椭圆的方程为 。
。
以O点为极点,x轴为极轴建立极坐标系,则椭圆的极坐标方程为 。
。
由于OA⊥OB,可设A(r1,q1), ,则
,则 ,
,
 ,
,
所以 ,
,
故 。
。
因为OM⊥AB,由等面积得|OM|·|AB|=|OA|·|OB|,
从而|OM|2·|AB|2=|OA|2·|OB|2,,且|AB|2=|OA|2+|OB|2,
即 ,所以
,所以 ,
,
故点M的轨迹是以O为圆心, 为半径的圆。
为半径的圆。
 。
。以O点为极点,x轴为极轴建立极坐标系,则椭圆的极坐标方程为
 。
。由于OA⊥OB,可设A(r1,q1),
 ,则
,则 ,
, ,
,所以
 ,
,故
 。
。因为OM⊥AB,由等面积得|OM|·|AB|=|OA|·|OB|,
从而|OM|2·|AB|2=|OA|2·|OB|2,,且|AB|2=|OA|2+|OB|2,
即
 ,所以
,所以 ,
,故点M的轨迹是以O为圆心,
 为半径的圆。
为半径的圆。
练习册系列答案
相关题目
 是
是 的内接四边形,
的内接四边形,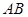 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
 ;
; 不是
不是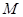 ,且
,且 ,证明:
,证明: 为等边三角形.
为等边三角形. 的左焦点为圆心,实轴长为半径的圆的标准方程为___________.
的左焦点为圆心,实轴长为半径的圆的标准方程为___________.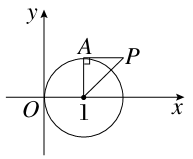
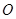 的割线
的割线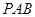 交圆
交圆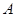 、
、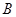 两点,割线
两点,割线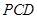 经过圆心
经过圆心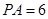 ,
,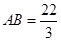 ,
,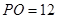 ,则圆
,则圆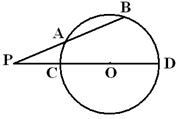
 中,以O为圆心的圆与直线
中,以O为圆心的圆与直线 相切.
相切. 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点 满足
满足 ,
, 的取值范围.
的取值范围.