题目内容
18.已知:|z-2i-1|=2,求|z-3|的最小值.分析 在复平面内|z-2i-1|=2表示C1(1,2)为圆心,以2为半径的圆.|z-3|表示点Z到(3,0)的距离,数形结合求其最小值.
解答 解:由|z-2i-1|=2,可得复数z在复平面内对应点Z的轨迹如图,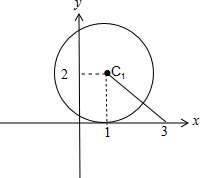
|z-3|表示点Z到(3,0)的距离,则$|z-3{|}_{min}=\sqrt{(3-1)^{2}+(0-2)^{2}}-2$=$2\sqrt{2}-2$.
点评 本题考查复数模的计算,利用其几何意义,采用数形结合的数学思想方法,是常用方法,是基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目