题目内容
18.如图是一个几何体的三视图(侧试图中的弧线是半圆),则该几何体的体积是( )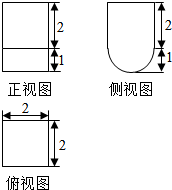
| A. | 8+2π | B. | 8+π | C. | 8+$\frac{2}{3}$π | D. | 8+$\frac{4}{3}$π |
分析 根据几何体的三视图,得出该几何体上半部分是正方体,下半部分是圆柱的一半,结合图中数据求出它的体积.
解答 解:根据几何体的三视图得,
该几何体的上半部分是棱长为2的正方体,
下半部分是半径为1,高为2的圆柱的一半,
∴该几何体的体积为
V=23+$\frac{1}{2}$×π×12×2=8+π.
故选:B.
点评 本题考查了利用三视图求几何体体积的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题.

练习册系列答案
相关题目
3.在△ABC中,三边长a,b,c,满足a+c=3b,则$tan\frac{A}{2}tan\frac{C}{2}$的值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.已知Sn是数列{an}的前n项和,且an=nsin$\frac{nπ}{3}$(n∈N*),则S50等于( )
| A. | -24$\sqrt{3}$ | B. | 24$\sqrt{3}$ | C. | -$\frac{75\sqrt{3}}{2}$ | D. | $\frac{51}{2}\sqrt{3}$ |
8.方程x2+y2cosα=1,α∈(0,π)表示的曲线不可能是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 直线 |