题目内容
8．方程x2+y2cosα=1，α∈（0，π）表示的曲线不可能是（ ）| A． | 圆 | B． | 椭圆 | C． | 双曲线 | D． | 直线 |
分析 求出cosα的范围，然后判断即可．
解答 解：α∈（0，π），cosα∈（-1，1），
当cosα∈（-1，0）时，方程x2+y2cosα=1表示双曲线．
当cosα=0时，方程x2+y2cosα=1表示直线；
当cosα∈（0，1）时，方程x2+y2cosα=1表示椭圆．
所以方程不可能表示圆．
故选：A．
点评 本题考查双曲线与椭圆的简单性质以及直线方程的形式，考查分类讨论以及计算能力．
练习册系列答案
相关题目
18．如图是一个几何体的三视图（侧试图中的弧线是半圆），则该几何体的体积是（ ）
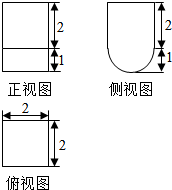
| A． | 8+2π | B． | 8+π | C． | 8+$\frac{2}{3}$π | D． | 8+$\frac{4}{3}$π |
19．若sin（π+α）+sin（-α）=-m，则sin（3π+α）+2sin（2π-α）等于（ ）
| A． | -$\frac{2}{3}$m | B． | -$\frac{3}{2}$m | C． | $\frac{2}{3}$m | D． | $\frac{3}{2}$m |
3．下列函数在区间（-1，1）上单调递减的是（ ）
| A． | y=cosx | B． | y=$\frac{1}{x-0.5}$ | C． | y=-ln（x+1） | D． | y=x+$\frac{1}{x}$ |
17．正三角形ABC的边长为2，将它沿高AD翻折，使点B与点C间的距离为$\sqrt{3}$，则四面体ABCD外接球的表面积为（ ）
| A． | 6π | B． | 7π | C． | 8π | D． | $\frac{{7\sqrt{7}}}{6}π$ |
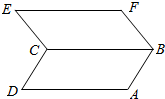如图所示，四边形ABCD和BCEF都是平行四边形．