题目内容
9.已知定义域为R的函数$f(x)=\frac{{-{2^x}-b}}{{{2^{x+1}}+2}}$是奇函数.(Ⅰ)求实数b的值;
(Ⅱ)判断并证明函数f(x)的单调性;
(Ⅲ)若关于x的方程f(x)=m在x∈[0,1]上有解,求实数m的取值范围.
分析 (1)根据f(0)=0求得b,再验证奇偶性;
(2)运用单调性的定义证明函数在R上单调递减;
(3)根据单调性确定函数的值域,由此得出参数的范围.
解答 解:(1)因为f(x)为R上的奇函数,所以,f(0)=0,
解得b=-1,f(x)=$\frac{1-2^x}{{2}^{x+1}+2}$,验证如下:
f(-x)+f(x)=$\frac{1}{2}$[$\frac{1-{2}^{-x}}{1+{2}^{x}}$+$\frac{1-2^x}{1+2^x}$]=0,
所以,f(-x)=-f(x),即f(x)为奇函数,
因此,b=-1;
(2)任取x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=-$\frac{1}{2}$[$\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}$-$\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$]=-$\frac{1}{2}$•$\frac{{2}^{{x}_{1}}-{2}^{{x}_{2}}}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$,
因为,x1<x2,所以,${2}^{{x}_{1}}-{2}^{{x}_{2}}$<0,
即f(x1)-f(x2)>0,所以,f(x)在R上单调递减;
(3)因为f(x)在[0,1]上单调递减,
所以,f(x)∈[f(1),f(0)]=[-$\frac{1}{6}$,0],
要使方程f(x)=m在x∈[0,1]上有解,
则m∈[-$\frac{1}{6}$,0].
点评 本题主要考查了函数奇偶性的性质,以及函数单调性的判断和证明,方程有解问题的解法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.数列{an}满足a1=1,Sn=n,则a2012=( )
| A. | 1 | B. | 2010 | C. | 2011 | D. | 2012 |
17.一个梯形采用斜二测画法作出其直观图,则其直观图的面积是原来梯形面积的( )
| A. | $\frac{\sqrt{2}}{4}$倍 | B. | $\frac{1}{2}$倍 | C. | $\frac{\sqrt{2}}{2}$倍 | D. | $\sqrt{2}$倍 |
4.给出下列四种说法:
(1)函数y=ax(a>0且a≠1)与函数$y={log_a}{a^x}(a>0$且a≠1)的定义域相同;
(2)函数y=x2与函数y=3x的值域相同;
(3)函数$y=\frac{1}{2}+\frac{1}{{{2^x}-1}}$与函数$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$均是定义在(-∞,0)∪(0,+∞)上的奇函数;
(4)函数y=(x-1)2与函数y=2x-1在(0,+∞)上都是奇函数.
其中正确说法的序号是( )
(1)函数y=ax(a>0且a≠1)与函数$y={log_a}{a^x}(a>0$且a≠1)的定义域相同;
(2)函数y=x2与函数y=3x的值域相同;
(3)函数$y=\frac{1}{2}+\frac{1}{{{2^x}-1}}$与函数$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$均是定义在(-∞,0)∪(0,+∞)上的奇函数;
(4)函数y=(x-1)2与函数y=2x-1在(0,+∞)上都是奇函数.
其中正确说法的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (3)(4) |
1.设a,b∈R,下列不等式中恒成立的是( )
| A. | $a+\frac{1}{a}≥2$ | B. | $\frac{a}{b}+\frac{b}{a}≥2$ | C. | a2+b2>2ab | D. | $\frac{{{a^2}+3}}{{\sqrt{{a^2}+2}}}>2$ |
18.如图是一个几何体的三视图(侧试图中的弧线是半圆),则该几何体的体积是( )
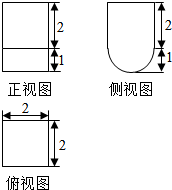

| A. | 8+2π | B. | 8+π | C. | 8+$\frac{2}{3}$π | D. | 8+$\frac{4}{3}$π |
19.若sin(π+α)+sin(-α)=-m,则sin(3π+α)+2sin(2π-α)等于( )
| A. | -$\frac{2}{3}$m | B. | -$\frac{3}{2}$m | C. | $\frac{2}{3}$m | D. | $\frac{3}{2}$m |
 已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.