题目内容
13.已知1≤lg(xy)≤4,-1$≤lg\frac{x}{y}$≤2,则lg$\frac{{x}^{2}}{y}$的取值范围是[-1,5].分析 由1≤lg(xy)≤4,-1$≤lg\frac{x}{y}$≤2,可得:1≤lgx+lgy≤4,-1≤lgx-lgy≤2,而lg$\frac{{x}^{2}}{y}$=2lgx-lgy,设2lgx-lgy=m(lgx+lgy)+n(lgx-lgy),利用“待定系数法”即可得出.
解答 解:由1≤lg(xy)≤4,-1$≤lg\frac{x}{y}$≤2,可得:1≤lgx+lgy≤4,-1≤lgx-lgy≤2,
而lg$\frac{{x}^{2}}{y}$=2lgx-lgy
设2lgx-lgy=m(lgx+lgy)+n(lgx-lgy),
∴$\left\{\begin{array}{l}{m+n=2}\\{m-n=-1}\end{array}\right.$,
解得m=$\frac{1}{2}$,n=$\frac{3}{2}$.
∴lg$\frac{{x}^{2}}{y}$=2lgx-lgy=$\frac{1}{2}$(lgx+lgy)+$\frac{3}{2}$(lgx-lgy),
∴-1≤$lg\frac{{x}^{2}}{y}$≤5,
故答案为:[-1,5].
点评 本题考查了不等式的性质、对数的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
4.给出下列四种说法:
(1)函数y=ax(a>0且a≠1)与函数$y={log_a}{a^x}(a>0$且a≠1)的定义域相同;
(2)函数y=x2与函数y=3x的值域相同;
(3)函数$y=\frac{1}{2}+\frac{1}{{{2^x}-1}}$与函数$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$均是定义在(-∞,0)∪(0,+∞)上的奇函数;
(4)函数y=(x-1)2与函数y=2x-1在(0,+∞)上都是奇函数.
其中正确说法的序号是( )
(1)函数y=ax(a>0且a≠1)与函数$y={log_a}{a^x}(a>0$且a≠1)的定义域相同;
(2)函数y=x2与函数y=3x的值域相同;
(3)函数$y=\frac{1}{2}+\frac{1}{{{2^x}-1}}$与函数$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$均是定义在(-∞,0)∪(0,+∞)上的奇函数;
(4)函数y=(x-1)2与函数y=2x-1在(0,+∞)上都是奇函数.
其中正确说法的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (3)(4) |
1.设a,b∈R,下列不等式中恒成立的是( )
| A. | $a+\frac{1}{a}≥2$ | B. | $\frac{a}{b}+\frac{b}{a}≥2$ | C. | a2+b2>2ab | D. | $\frac{{{a^2}+3}}{{\sqrt{{a^2}+2}}}>2$ |
18.如图是一个几何体的三视图(侧试图中的弧线是半圆),则该几何体的体积是( )
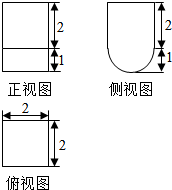

| A. | 8+2π | B. | 8+π | C. | 8+$\frac{2}{3}$π | D. | 8+$\frac{4}{3}$π |
3.下列函数在区间(-1,1)上单调递减的是( )
| A. | y=cosx | B. | y=$\frac{1}{x-0.5}$ | C. | y=-ln(x+1) | D. | y=x+$\frac{1}{x}$ |