题目内容
已知函数y=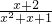
（x＞-2）
（1）求
的取值范围；
（2）当x为何值时，y取何最大值？
解：（1）设：x+2=t，x=t-2，t＞0，
则：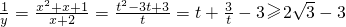
，
∴的取值范围为[2
-3，++∞）；
（2）欲使y最大，必定最小，
此时t=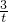
，可得t=，即x=2+，ymax=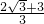
∴当x=2+时，y最大值为．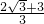
分析：（1）先设：x+2=t，则：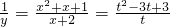
，再利用基本不等式求出其取值范围；
（2）欲使y最大，必定最小，由（1）可知，此时t=，即x=2+，ymax=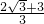，从而得y的最大值．
点评：本题考查利用基本不等式求函数的最值时，必须注意满足的条件：一正、二定、三相等．
则：
，∴
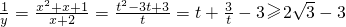的取值范围为[2-3，++∞）；（2）欲使y最大，必定
最小，此时t=
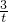，可得t=，即x=2+，ymax=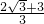∴当x=2+
时，y最大值为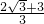．分析：（1）先设：x+2=t，则：
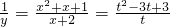，再利用基本不等式求出其取值范围；（2）欲使y最大，必定
最小，由（1）可知，此时t=，即x=2+，ymax=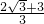，从而得y的最大值．点评：本题考查利用基本不等式求函数的最值时，必须注意满足的条件：一正、二定、三相等．
练习册系列答案
相关题目